题目内容

4．已知函数f（x）=alog2x+blog3x+2，且f（$\frac{1}{2015}$）=-1，则f（2015）=（　　）
A．2B．3C．4D．5

分析 根据f（$\frac{1}{2015}$）=-1列出式子，利用对数的运算求出alog22015+blog32015=3，代入f（2015）求值即可．

解答 解：∵函数f（x）=alog2x+blog3x+2，且f（$\frac{1}{2015}$）=-1，
∴alog2$\frac{1}{2015}$+blog3$\frac{1}{2015}$+2=-1，则-alog22015-blog32015+2=-1，
即alog22015+blog32015=3，
∴f（2015）=alog22015+blog32015+2=5，
故选：D．

点评 本题考查利用整体代换求函数值，以及对数的运算性质的应用，属于基础题．

练习册系列答案
相关题目
18．已知数列{an}中，a2=3，a4=15，若{an+1}为等比数列，则a6等于（　　）
A．63B．64C．75D．65
19．将2枚质地均匀的骰子抛掷一次，记向上的点数分别为a、b，则事件“a+b=5”的概率为（　　）
A．$\frac{1}{2}$B．$\frac{1}{3}$C．$\frac{1}{6}$D．$\frac{1}{9}$
12．安排甲、乙、丙、丁四人参加周一至周六的公益活动，每天只需一人参加，其中甲参加三天活动，乙、丙、丁每人参加一天，那么甲连续三天参加活动的概率为（　　）
A．$\frac{1}{15}$B．$\frac{1}{5}$C．$\frac{1}{4}$D．$\frac{1}{2}$
19．在平面直角坐标系xOy中，已知曲线C1：$\left\{\begin{array}{l}{x=1-t}\\{y=2t+1}\end{array}\right.$（t为参数）与曲线C2：$\left\{\begin{array}{l}{x=2cosθ}\\{y=bsinθ}\end{array}\right.$（θ为参数，b＞0）有一个公共点在y轴，则b=3．
9．已知f（n）=1+$\frac{1}{{2}^{2}}$+$\frac{1}{{3}^{2}}$+…+$\frac{1}{{n}^{2}}$，g（n）=$\frac{1}{2}$（3-$\frac{1}{{n}^{2}}$），n∈N*．
（1）当n=1，2，3时，试比较f（n）与g（n）的大小关系；
（2）猜想f（n）与g（n）的大小关系，并用数学归纳法证明．
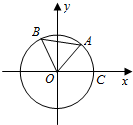16．如图，点A，B是单位圆上的两点，A，B两点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，若点A的坐标为（$\frac{3}{5}$，$\frac{4}{5}$），记∠COA=α．
（Ⅰ）求$\frac{1+sin2α}{1+cos2α}$的值；
（Ⅱ）求cos∠COB的值．
13．已知椭圆的方程为$\frac{{x}^{2}}{{a}^{2}}$+y2=1（a＞1），上顶点为A，左顶点为B，设P是椭圆上的任一点，则△PAB的最大值为$\sqrt{2}$+1，若已知M（-$\sqrt{3}$，0），N（$\sqrt{3}$，0），点Q为椭圆上的任意一点，则$\frac{1}{|QN|}+\frac{4}{|QM|}$的最小值为$\frac{9}{4}$．
14．若二项式（x2-$\frac{2}{x}$）n展开式的第5项是常数项，则展开式的中间项为（　　）
A．-160B．-160x3C．20D．160x3

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网