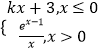题目内容
【题目】已知![]() 是椭圆
是椭圆![]() 与抛物线
与抛物线![]() 的一个公共点,且椭圆与抛物线具有一个相同的焦点
的一个公共点,且椭圆与抛物线具有一个相同的焦点![]() .
.
(1)求椭圆![]() 及抛物线
及抛物线![]() 的方程;
的方程;
(2)设过![]() 且互相垂直的两动直线
且互相垂直的两动直线![]() ,
,![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点,求四边形
两点,求四边形![]() 面积的最小值
面积的最小值
【答案】(Ⅰ)椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() ;(Ⅱ)见解析.
;(Ⅱ)见解析.
【解析】
(1)先求![]() ,即得c,再将点P坐标代入椭圆方程,解方程组得a,b,即得结果,(2)根据垂直条件得
,即得c,再将点P坐标代入椭圆方程,解方程组得a,b,即得结果,(2)根据垂直条件得![]() ,设直线
,设直线![]() 的方程
的方程![]() ,与椭圆方程联立方程,结合韦达定理以及弦长公式解得AB,类似可得CD,最后根据二次函数性质求最值.
,与椭圆方程联立方程,结合韦达定理以及弦长公式解得AB,类似可得CD,最后根据二次函数性质求最值.
(Ⅰ)![]() 抛物线
抛物线![]() :
:![]() 一点
一点
![]() ,即抛物线
,即抛物线![]() 的方程为
的方程为![]() ,
,![]()
![]()
又![]() 在椭圆
在椭圆![]() :
:![]() 上
上
![]() ,结合
,结合![]() 知
知![]() (负舍),
(负舍), ![]() ,
,
![]() 椭圆
椭圆![]() 的方程为
的方程为![]() ,抛物线
,抛物线![]() 的方程为
的方程为![]() .
.
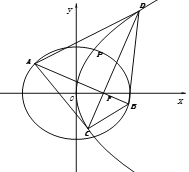
(Ⅱ)由题可知直线![]() 斜率存在,设直线
斜率存在,设直线![]() 的方程
的方程![]() ,
,![]()
①当![]() 时,
时,![]() ,直线
,直线![]() 的方程
的方程![]() ,
,![]() ,故
,故![]()
②当![]() 时,直线
时,直线![]() 的方程为
的方程为![]() ,由
,由 得
得![]() .
.
![]()
由弦长公式知![]()
![]() .
.
同理可得![]() .
.
![]() .
.
令![]() ,则
,则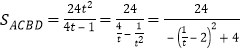 ,当
,当![]() 时,
时,![]() ,
,![]()
综上所述:四边形![]() 面积的最小值为8.
面积的最小值为8.

练习册系列答案
 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目