��Ŀ����
����Ŀ������ͬѧ��7����13��ÿ������ʱ���Լ������߲������¼�����
���� ���꣩ | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
���� ��cm�� | 121 | 128 | 135 | 141 | 148 | 154 | 160 |
����������y��������x�����Իع鷽�̣�
�������ã����е����Իع鷽�̣���������ͬѧ7����13�����ߵı仯�������17��֮ǰ��������һ�仯����Ԥ������ͬѧ15��ʱ�����ߣ�
�����ع�ֱ�ߵ�б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��![]() =
= 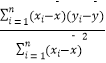 ��
�� ![]() ��
��
���𰸡��⣺����������� ![]() =
= ![]() ��7+8+9+10+11+12+13��=10��
��7+8+9+10+11+12+13��=10�� ![]() =
= ![]() ��121+128+135+141+148+154+160��=141��
��121+128+135+141+148+154+160��=141��![]() ��
�� ![]() =9+4+1+0+1+4+9=28��
=9+4+1+0+1+4+9=28��![]() ��xi��
��xi�� ![]() ����yi��
����yi�� ![]() ��=����3��������20��+����2��������13��+����1��������6��+0��0+1��7+2��13+3��19=182��
��=����3��������20��+����2��������13��+����1��������6��+0��0+1��7+2��13+3��19=182��
���� ![]() =
= ![]() =
= ![]() ��
�� ![]() =141��
=141�� ![]() ��10=76��
��10=76��
����ع鷽��Ϊ ![]() =
= ![]() x+76��
x+76��
�����ɣ���֪�� ![]() =
= ![]() ��0��
��0��
������ͬѧ7����13�������ÿ�궼�����ߣ�ƽ��ÿ������6.5cm��
��x=15���루���еĻع鷽�̣��� ![]() =
= ![]() ��15+76=173.5��
��15+76=173.5��
��Ԥ������ͬѧ15�������Ϊ173.5cm��
���������������ȸ��ݱ����빫ʽ���������ݣ�Ȼ��������Իع鷽����� ![]() ���ɴ�������Իع鷽�̣�������15���루���еĻع鷽�̼����������ͬѧ15��ʱ�����ߣ�
���ɴ�������Իع鷽�̣�������15���루���еĻع鷽�̼����������ͬѧ15��ʱ�����ߣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�