题目内容
19.在直角坐标平面内,曲线C的参数方程为$\left\{\begin{array}{l}x=rcosα\\ y=rsinα\end{array}\right.$(r>0,α为参数),以坐标原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知点A、B的极坐标分别为$(2\;,\;\frac{2π}{3})$、(2,π),若直线AB和曲线C只有一个公共点,则r=$\sqrt{3}$.分析 化圆的参数方程为普通方程,化直线的极坐标方程为直角坐标方程,由圆心到直线的距离等于圆的半径得答案.
解答 解:由$\left\{\begin{array}{l}x=rcosα\\ y=rsinα\end{array}\right.$,得x2+y2=r2.
由A$(2\;,\;\frac{2π}{3})$、B(2,π),得A(-1,$\sqrt{3}$),B(-2,0).
∴直线AB的方程为$\frac{y}{\sqrt{3}}=\frac{x+2}{-1+2}$,整理得:$y=\sqrt{3}x+2\sqrt{3}$.
∵直线AB和曲线C只有一个公共点,∴$\frac{|2\sqrt{3}|}{\sqrt{(\sqrt{3})^{2}+(-1)^{2}}}=\sqrt{3}=r$.
故答案为:$\sqrt{3}$.
点评 本题考查参数方程化普通方程,考查极坐标方程化直角坐标方程,训练了点到直线距离公式的应用,是基础的计算题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.已知向量|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=2,$\overrightarrow a$与$\overrightarrow b$的夹角为$\frac{π}{3}$.若向量$\overrightarrow m$满足|$\overrightarrow{m}$-$\overrightarrow{a}$-$\overrightarrow{b}$|=1,则$|{\overrightarrow m}$|的最大值是( )
| A. | 2$\sqrt{3}$-1 | B. | 2$\sqrt{3}$+1 | C. | 4 | D. | $\sqrt{6}+\sqrt{2}$+1 |
4.已知角α终边与单位圆x2+y2=1的交点为$P(\frac{1}{2},y)$,则$sin(\frac{π}{2}+2α)$=( )
| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
11.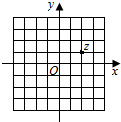 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
 若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )
若i为虚数单位,图中网格纸的小正方形的边长是1,复平面内点Z表示复数z,那么复数$\frac{z}{1+i}$对应的点位于复平面内的( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
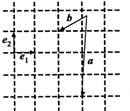 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.