题目内容
14.设函数f(x)=lnx+ax2+bx(a,b∈R),其图象在点(1,f(1))处的切线平行于x轴.(Ⅰ)若a=1,求函数f(x)的极值;
(Ⅱ)试讨论函数f(x)的单调性.
分析 (Ⅰ)先求出函数f(x)的导数,将a=1代入,求出f′(x)=0的根,从而求出函数的单调性,求出函数的极值;
(Ⅱ)先求出函数f(x)的导数,通过讨论a的范围,从而求出的单调性.
解答 解:(Ⅰ)f(x)=lnx+ax2+bx 的定义域为(0,+∞),f′(x)=2ax+$\frac{1}{x}$+b,
∵图象在点(1,f(1))处的切线平行于x轴,
∴f′(1)=2a+b+1=0,b=-2a-1,
f′(x)=2ax+$\frac{1}{x}$-2a-1=$\frac{(2ax-1)(x-1)}{x}$,
当a=1时,$f'(x)=\frac{(2x-1)(x-1)}{x}=0,{x_1}=\frac{1}{2},{x_2}=1$.
当$0<x<\frac{1}{2}$时,f′(x)>0,f(x)单调增;
$\frac{1}{2}<x<1$时,f′(x)<0,f(x)单调减;
x>1时,f′(x)>0,f(x)单调增.
∴f(x)的极大值为$f(\frac{1}{2})=-\frac{5}{4}-ln2$,f(x)的极小值为f(1)=-2.
(Ⅱ)由(Ⅰ)知:$f'(x)=2ax+\frac{1}{x}-2a-1=\frac{(2ax-1)(x-1)}{x}$.
∴a≤0时,x∈(0,1)f′(x)>0,f(x)单调增,x∈(1,+∞)f′(x)<0,f(x)单调减;
$0<a<\frac{1}{2}$时,x∈(0,1)f′(x)>0,f(x)单调增,$x∈(1,\frac{1}{2a})$f′(x)<0,f(x)单调减,
$x∈(\frac{1}{2a},+∞)$f′(x)>0,f(x)单调增;
$a=\frac{1}{2}$时,x∈(0,+∞)f′(x)>0,f(x)单调增;
$a>\frac{1}{2}$时,$x∈(0,\frac{1}{2a})$f′(x)>0,f(x)单调增,$x∈(\frac{1}{2a},1)$f′(x)<0,f(x)单调减,
x∈(1,+∞)f′(x)>0,f(x)单调增.
点评 本题考查了函数的单调性,考察导数的应用,考查分类讨论思想,是一道中档题.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | $-\frac{{\sqrt{3}}}{2}$ | D. | 1 |
| A. | $({0,\frac{1}{2}})$ | B. | $({0,\frac{{\sqrt{2}}}{4}})∪({\frac{{\sqrt{2}}}{4},\frac{1}{2}})$ | C. | $({\frac{{\sqrt{2}}}{4},+∞})$ | D. | $[{\frac{1}{2},2\sqrt{2}}]$ |
| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
| A. | (-1,0) | B. | (1,+∞) | C. | (-1,0)∪(1,+∞) | D. | (-∞,-1)∪(1,+∞) |
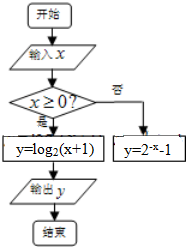
| A. | [0,2] | B. | [1,2] | C. | [0,1] | D. | [-1,5] |
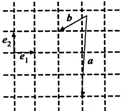 已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.
已知向量$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$、$\overrightarrow{a}$、$\overrightarrow{b}$如图所示,以$\overrightarrow{{e}_{1}}$、$\overrightarrow{{e}_{2}}$为基底,则$\overrightarrow{a}$-$\overrightarrow{b}$可表示为$\overrightarrow{{e}_{1}}$-3$\overrightarrow{{e}_{2}}$.