题目内容
【题目】在平面直角坐标系中，以原点为极点，x轴的非负半轴为极轴，并在两坐标系中取相同的长度单位，若直线l的极坐标方程是ρsin（θ+ 
）=2 
，且点P是曲线C： 
（θ为参数）上的一个动点．
（Ⅰ）将直线l的方程化为直角坐标方程；
（Ⅱ）求点P到直线l的距离的最大值与最小值．
【答案】解：（Ⅰ）∵直线l的极坐标方程是ρsin（θ+ 
）=2 
，
∴ 
，
∴ρsinθ+ρcosθ=4，
由ρsinθ=y，ρcosθ=x，得x+y=4．
∴直线l的直角坐标方程为x+y=4．
（Ⅱ）∵点P是曲线C： 
（θ为参数）上的一个动点，
∴P（ 
），
点P到直线l的距离d=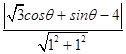 
= 
，
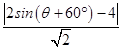∴点P到直线l的距离的最大值dmax= 
=3 ，
点P到直线l的距离的最小值dmin= 
= ．
【解析】（Ⅰ）直线l的极坐标方程转化为ρsinθ+ρcosθ=4，由ρsinθ=y，ρcosθ=x，能求出直线l的直角坐标方程．（Ⅱ）由题意P（ 
），从而点P到直线l的距离d= 
= 
，由此能求出点P到直线l的距离的最大值与最小值．
练习册系列答案
相关题目
