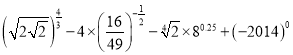Question

【题目】已知动圆M恒过点（0，1），且与直线y=﹣1相切．
（1）求圆心M的轨迹方程；
（2）动直线l过点P（0，﹣2），且与点M的轨迹交于A、B两点，点C与点B关于y轴对称，求证：直线AC恒过定点．

Answer 1

【答案】
（1）解：∵动点M到直线y=﹣1的距离等于到定点C（0，1）的距离，

∴动点M的轨迹为抛物线，且 =1，解得：p=2，

∴动点M的轨迹方程为x2=4y

（2）解：证明：由题意可知直线l的斜率存在，

设直线l的方程为：y=kx﹣2，A（x1，y1），B（x2，y2），则C（﹣x2，y2）．

联立 ，化为x2﹣4kx+8=0，

△=16k2﹣32＞0，

解得k＞ 或k＜﹣ ．

∴x1+x2=4k，x1x2=8．

直线直线AC的方程为：y﹣y2=﹣ （x+x2），

又∵y1=kx1﹣2，y2=kx2﹣2，

∴4ky﹣4k（kx2﹣2）=（kx2﹣kx1）x+kx1x2﹣kx22，

化为4y=（x2﹣x1）x+x2（4k﹣x2），

∵x1=4k﹣x2，

∴4y=（x2﹣x1）x+8，

令x=0，则y=2，

∴直线AC恒过一定点（0，2）

【解析】（1）由题意可知圆心M的轨迹为以（0，1）为焦点，直线y=﹣1为准线的抛物线，根据抛物线的方程即可求得圆心M的轨迹方程；（2）由题意可知直线l的斜率存在，设直线l的方程为：y=kx﹣2，A（x1，y1），B（x2，y2），则C（﹣x2，y2）．代入抛物线方，由韦达定理及直线直线AC的方程为：y﹣y2=﹣ （x+x2），把根与系数的关系代入可得4y=（x2﹣x1）x+8，令x=0，即可得出直线恒过定点．