题目内容
【题目】点A,B,C,D在同一个球的球面上,AB=BC= ![]() ,∠ABC=90°,若四面体ABCD体积的最大值为3,则这个球的表面积为( )
,∠ABC=90°,若四面体ABCD体积的最大值为3,则这个球的表面积为( )
A.2π
B.4π
C.8π
D.16π
【答案】D
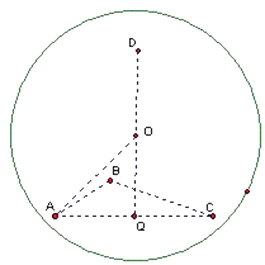
【解析】解:根据题意知,直角三角形△ABC的面积为3.其所在球的小圆的圆心在斜边AC的中点上,设小圆的圆心为Q,
若四面体ABCD的体积的最大值,由于底面积S△ABC不变,高最大时体积最大,
所以,DQ与面ABC垂直时体积最大,最大值为为 ![]() S△ABC×DQ=3,
S△ABC×DQ=3,
即 ![]() ×3×DQ=3,∴DQ=3,如图.设球心为O,半径为R,则在直角△AQO中,
×3×DQ=3,∴DQ=3,如图.设球心为O,半径为R,则在直角△AQO中,
OA2=AQ2+OQ2,即R2=( ![]() )2+(3﹣R)2,∴R=2,
)2+(3﹣R)2,∴R=2,
则这个球的表面积为:S=4π×22=16π.
故选:D.
根据几何体的特征,判定外接球的球心,求出球的半径,即可求出球的表面积

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目