题目内容
【题目】若函数y=f（x）的图象上存在不同两点M、N关于原点对称，则称点对[M，N]是函数y=f（x）的一对“和谐点对”（点对[M，N]与[N，M]看作同一对“和谐点对”）．已知函数f（x）= 
则此函数的“和谐点对”有（ ）
A.0对
B.1对
C.2对
D.4对
【答案】B
【解析】解：若f（x）=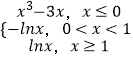 
，
令f（x）+f（﹣x）=0，
若0＜x＜1，则﹣lnx﹣x3+3x=0，即lnx=﹣x3+3x，
作出y=lnx与y=﹣x3+3x的函数图象，
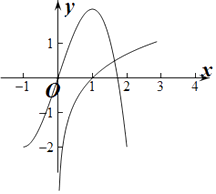
由图象可知两函数在（0，1）上无交点，
若x≥1，则lnx﹣x3+3x=0，即lnx=x3﹣3x，
作出y=lnx与y=x3﹣3x的函数图象，
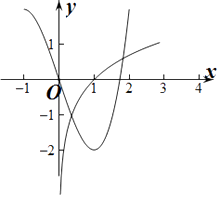
由图象可知两函数在（1，+∞）上有1个交点，
所以，f（x）只有1对“和谐点对”．
故选B．
【考点精析】本题主要考查了函数的图象的相关知识点，需要掌握函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值才能正确解答此题．
练习册系列答案
相关题目
