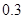题目内容
（本小题满分12分）
质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4。将4个这样的玩具同时抛掷于桌面上。
(Ⅰ)设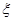
为与桌面接触的4个面上数字中偶数的个数，求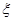的分布列及期望E；
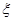(Ⅱ)求与桌面接触的4个面上的4个数的乘积能被4整除的概率。
质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4。将4个这样的玩具同时抛掷于桌面上。
(Ⅰ)设
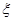为与桌面接触的4个面上数字中偶数的个数，求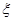的分布列及期望E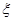；(Ⅱ)求与桌面接触的4个面上的4个数的乘积能被4整除的概率。
(Ⅰ)
E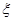
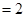
(Ⅱ)
E
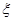
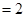
(Ⅱ)
本试题主要是考查了概率的分布列的求解和数学期望值的运用。以及古典概型概率的运用。
（1）由于质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4。将4个这样的玩具同时抛掷于桌面上，则设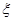为与桌面接触的4个面上数字中偶数的个数服从二项分布，因此可得到结论。
（2）因为不能被4整除的有两种情影：
①4个数均为奇数，概率为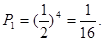
②4个数中有3个奇数，另一个为2，概率为
分类讨论得到结论。
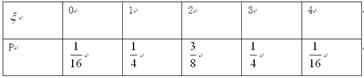
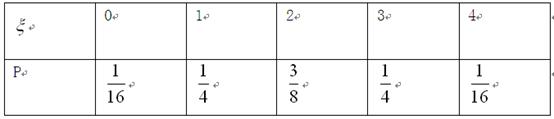
解：(Ⅰ)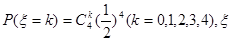
的分布列为
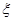服从二项分布
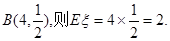………6分
(Ⅱ)不能被4整除的有两种情影：
①4个数均为奇数，概率为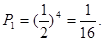
②4个数中有3个奇数，另一个为2，概率为
故所求的概率为P
………12分
（1）由于质地均匀的正四面体玩具的4个面上分别刻着数字1，2，3，4。将4个这样的玩具同时抛掷于桌面上，则设
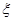为与桌面接触的4个面上数字中偶数的个数服从二项分布，因此可得到结论。（2）因为不能被4整除的有两种情影：
①4个数均为奇数，概率为
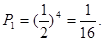
②4个数中有3个奇数，另一个为2，概率为
分类讨论得到结论。
解：(Ⅰ)
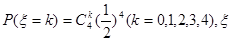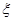的分布列为服从二项分布 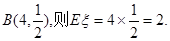………6分(Ⅱ)不能被4整除的有两种情影：
①4个数均为奇数，概率为
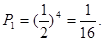
②4个数中有3个奇数，另一个为2，概率为
故所求的概率为P
………12分
练习册系列答案
阅读快车系列答案
相关题目
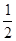，他的命中率与目标距离的平方成反比，且各次射击都是独立的。
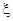的概率分布率由下图给出：
）：
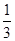
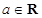=_______，方差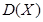
=____________.
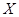的分布列如右表．若
，
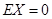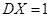，则
，
．
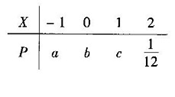
的分布列如下表所示，
，则
的值等于 ； 
的分布如图所示则数学期望
．
