题目内容
某项新技术进入试用阶段前必须对其中三项不同指标甲、乙、丙进行通过量化检测。假设该项新技术的指标甲、乙、丙独立通过检测合格的概率分别为 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
(Ⅰ)求该项技术量化得分不低于8分的概率;
(Ⅱ)记该技术的三个指标中被检测合格的指标个数为随机变量 ,求
,求 的分布列与数学期望。
的分布列与数学期望。
 ,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。
,指标甲、乙、丙检测合格分别记4分、2分、4分,若某项指标不合格,则该项指标记0分,各项指标检测结果互不影响。(Ⅰ)求该项技术量化得分不低于8分的概率;
(Ⅱ)记该技术的三个指标中被检测合格的指标个数为随机变量
 ,求
,求 的分布列与数学期望。
的分布列与数学期望。(Ⅰ)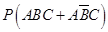
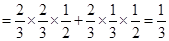
(Ⅱ)随机变量 的分布列
的分布列
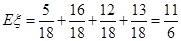
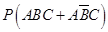
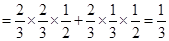
(Ⅱ)随机变量
 的分布列
的分布列 | 0 | 1 | 2 | 3 |
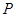 |  | 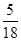 | 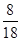 | 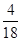 |
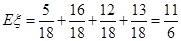
本试题主要是考查了独立事件概率的乘法公式和互斥事件概率的加法公式的运用,记忆分布列的求解和数学期望值的运算的综合运用。
(1)根据已知条件分析清楚该项技术量化得分不低于8分的事件为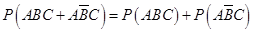 ,然后借助于独立事件的乘法公式得到。
,然后借助于独立事件的乘法公式得到。
(2)分析随机变量的取值情况和各个取值的概率值,然后得到分布列和数学期望值的运算,并能结合对立事件和互斥事件准确表示概率值是解决该试题的关键解:(Ⅰ)记该项新技术的三个指标甲、乙、丙独立通过检测合格分别为事件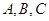 ,则事件“得分不低于8分”表示为
,则事件“得分不低于8分”表示为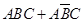 .因为
.因为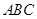 和为互斥事件
和为互斥事件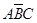 ,且
,且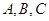 彼此独立,
彼此独立,
所以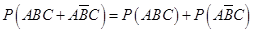
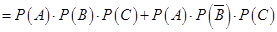
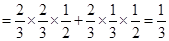 ……………………………5分
……………………………5分
(Ⅱ)该技术的三个指标中被检测合格的指标个数 的取值为
的取值为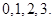
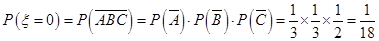 …………………7分
…………………7分
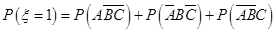
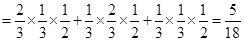

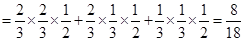
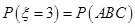
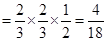
所以,随机变量 的分布列
的分布列
所以,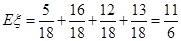
(1)根据已知条件分析清楚该项技术量化得分不低于8分的事件为
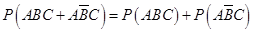 ,然后借助于独立事件的乘法公式得到。
,然后借助于独立事件的乘法公式得到。(2)分析随机变量的取值情况和各个取值的概率值,然后得到分布列和数学期望值的运算,并能结合对立事件和互斥事件准确表示概率值是解决该试题的关键解:(Ⅰ)记该项新技术的三个指标甲、乙、丙独立通过检测合格分别为事件
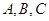 ,则事件“得分不低于8分”表示为
,则事件“得分不低于8分”表示为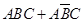 .因为
.因为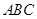 和为互斥事件
和为互斥事件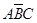 ,且
,且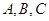 彼此独立,
彼此独立,所以
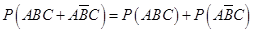
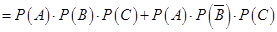
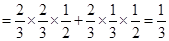 ……………………………5分
……………………………5分(Ⅱ)该技术的三个指标中被检测合格的指标个数
 的取值为
的取值为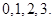
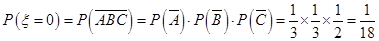 …………………7分
…………………7分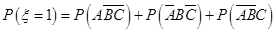
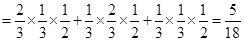

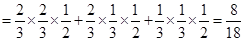
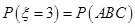
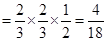
所以,随机变量
 的分布列
的分布列 | 0 | 1 | 2 | 3 |
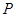 |  | 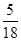 | 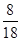 | 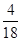 |
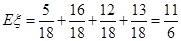

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
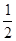 ,他的命中率与目标距离的平方成反比,且各次射击都是独立的。
,他的命中率与目标距离的平方成反比,且各次射击都是独立的。 的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。
的分布列;(2)求双方组织者通过比赛获得总收益的数学期望。

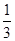
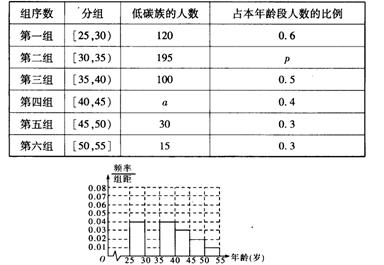
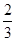 ,乙获胜的概率为
,乙获胜的概率为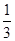 ,假定各次比赛相互独立,比赛经ξ次结束,求:
,假定各次比赛相互独立,比赛经ξ次结束,求: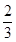 ,被乙小组攻克的概率为
,被乙小组攻克的概率为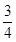 ,
,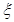 为攻关期满时获奖的攻关小组数,求
为攻关期满时获奖的攻关小组数,求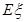 ;
;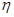 为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数
为攻关期满时获奖的攻关小组数与没有获奖的攻关小组数之差的平方,记“函数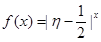 在定义域内单调递增”为事件C,求事件C发生的概率;
在定义域内单调递增”为事件C,求事件C发生的概率; 的分布列如下表所示,
的分布列如下表所示, ,则
,则 的值等于 ;
的值等于 ; 