题目内容
（本小题满分12分）
一个口袋内有
(
)个大小相同的球，其中有3个红球和
个白球．已知从口袋中随机取出一个球是红球的概率是
．
(1)当
时，不放回地从口袋中随机取出3个球，求取到白球的个数
的期望
；
(2)若
，有放回地从口袋中连续地取四次球(每次只取一个球)，在四次摸球中恰好取到两次红球的概率大于
，求和．
一个口袋内有
()个大小相同的球，其中有3个红球和个白球．已知从口袋中随机取出一个球是红球的概率是． (1)当
时，不放回地从口袋中随机取出3个球，求取到白球的个数的期望；(2)若
，有放回地从口袋中连续地取四次球(每次只取一个球)，在四次摸球中恰好取到两次红球的概率大于，求和．解：(I)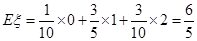
． (II) 
．
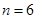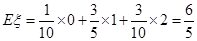． (II) 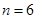． 本试题主要是考查了古典概型概率的运算，以及分布列的求解和不等式的综合运用。
（1）因为口袋内有()个大小相同的球，其中有3个红球和个白球．已知从口袋中随机取出一个球是红球的概率是
，因此得到n的值，然后利用古典概型概率得到结论。
（2）由题设知，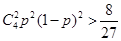
，解不等式得到p的范围，结合p的值
，可知p的值，和n的值的求解。
解：(I)，所以5个球中有2个白球
白球的个数可取0，1，2． ········· 1分
．······· 4分
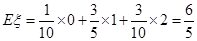． ······ 6分
(II)由题设知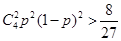，， ····· 8分
因为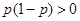
所以不等式可化为
，
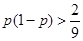解不等式得，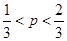
，即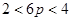
． ······ 10分
又因为，所以
，即
，
所以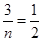，所以
，所以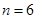． ······· 12分
（1）因为口袋内有
()个大小相同的球，其中有3个红球和个白球．已知从口袋中随机取出一个球是红球的概率是，因此得到n的值，然后利用古典概型概率得到结论。（2）由题设知，
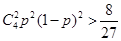，解不等式得到p的范围，结合p的值，可知p的值，和n的值的求解。解：(I)
，所以5个球中有2个白球白球的个数
可取0，1，2． ········· 1分．······· 4分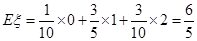． ······ 6分(II)由题设知，
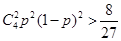， ····· 8分因为
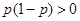所以不等式可化为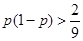，解不等式得，
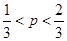，即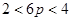． ······ 10分又因为
，所以，即，所以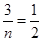
，所以，所以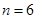． ······· 12分
练习册系列答案
相关题目
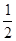，他的命中率与目标距离的平方成反比，且各次射击都是独立的。
，则E
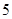枚均匀的硬币
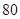次，设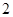
枚正面向上，
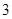枚反面向上的次数为
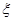，则
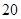
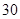
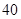
，乙获胜的概率为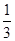
，假定各次比赛相互独立，比赛经ξ次结束，求：
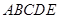五个不同区域，要求同一区域上用同一种颜色的鲜花，相邻区域使用不同颜色的鲜花.现有红、黄、蓝、白、紫五种不同颜色的鲜花可供任意选择．
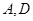区域同时用红色鲜花时，求布置花圃的不同方法的种数；
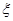为花圃中用红色鲜花布置的区域的个数，求随机变量