题目内容

1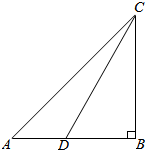．如图，一人在某山脚B的正西方向A处测得山顶C的仰角为45°，再向正东方向行进（3-$\sqrt{3}$）百米后到D，测得山顶C在D的北偏东30°，则该山BC的高度为（　　）百米．
A．1B．2C．3D．4

分析 由题意可得：AB=BC，tan∠CDB=tan60°=$\sqrt{3}$=$\frac{CB}{DB}$，解得DB=$\frac{CB}{\sqrt{3}}$，由AD+DB=3$-\sqrt{3}$+$\frac{CB}{\sqrt{3}}$=BC，即可解得BC的值．

解答 解：由题意可得：∠CAB=45°，AD=3-$\sqrt{3}$，∠CDB=60°，∠CBA=90°，
可得：AB=BC，
故在△CDB中，tan∠CDB=tan60°=$\sqrt{3}$=$\frac{CB}{DB}$，解得DB=$\frac{CB}{\sqrt{3}}$，
所以：AD+DB=3$-\sqrt{3}$+$\frac{CB}{\sqrt{3}}$=BC，解得：BC=3．
故选：C．

点评 本题考查了解直角三角形的应用，仰角俯角问题的应用，根据三角函数的定义用CB表示出DB是解题关键，属于中档题．

练习册系列答案
相关题目
11．若椭圆$\frac{{x}^{2}}{3m+12}$-$\frac{{y}^{2}}{m}$=1的准线平行于y轴，则m的取值范围是-3＜m＜0．
12．设E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的焦点为F1，F2，点P为E上一动点，∠F1PF2=2θ．
（1）证明：当点P为短轴端点时∠F1PF2取最大值．
（2）若∠F1PF2=90°，求∠F1PF2的面积；
（3）求证：△F1PF2的面积S=b2tanθ．
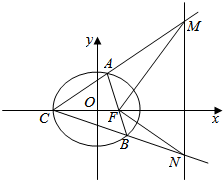9．如图，已知椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的右焦点F与抛物线y2=4x的焦点重合，D（1，$\frac{3}{2}$）是椭圆上一点，椭圆左顶点为C，过F的直线与椭圆交于A、B两点，直线CA、CB与直线1：x=4交于点M、N．
（I）求椭圆的方程；
（Ⅱ）求$\overrightarrow{FM}$•$\overrightarrow{FN}$的值．
16．抛物线C：y=x2在点P处的切线l分别交x轴、y轴于不同的两点A、B，$\overrightarrow{AM}=\frac{1}{2}\overrightarrow{MB}$．当点P在C上移动时，点M的轨迹为D．
（1）求曲线D的方程；
（2）设直线l与曲线D的另一个交点为N，曲线D在点M、N处的切线分别为m、n，直线m、n相交于点Q．证明：PQ平行于x轴．
6．当x∈[-1，t]时，函数f（x）=|x-2|+|5-x|的值域为[3，9]，则实数t的取值范围是（　　）
A．[2，8]B．[2，4]C．[4，8]D．[-1，5]
13．已知函数f（x）=mx-（m+2）lnx-$\frac{2}{x}$，g（x）=x2+mx+1，其中m＜0．
（1）求f（x）的单调区间；
（2）若存在x1、x2∈[1，2]，使得f（x1）-g（x2）≥1成立．求m的取值范围．
10．设函数f（x）=lnx+a（x2-1）-2（x-1）．
（Ⅰ）若a=0时直线y=mx+1与曲线y=f（x）相切，求m的值；
（Ⅱ）已知（x-1）f（x）≥0，求a的取值范围．
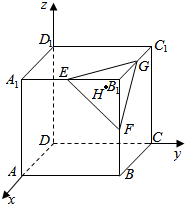14．如图，在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1，E，F，G，分别为A1B1，B1C1，BB1的中点，H为△EFG的重心，求DH的长度．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网