题目内容
9.已知椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{16}$=1,AB为过焦点的弦,求|AB|的最大值和最小值.分析 可想着写出AB的方程,从而可讨论斜率k是否存在:不存在斜率时,容易得出|AB|=$\frac{32}{5}$;而存在斜率时,可以设直线AB的方程为y=k(x-3),联立椭圆的方程,从而可消去y得到关于x的方程,(25k2+16)x2-150k2x+225k2-400=0,根据韦达定理可写出x1+x2,x1x2,由弦长公式即可求出|AB|=$\frac{32}{5}+\frac{288}{5(25{k}^{2}+16)}$,这样由k2≥0即可得出|AB|的范围,从而可得出|AB|的最大值和最小值.
解答 解:椭圆的右焦点为(3,0),则:
(1)若过该焦点的直线不存在斜率,则该直线方程为x=3,带入椭圆方程得:
$\frac{9}{25}+\frac{{y}^{2}}{16}=1$;
∴$y=±\frac{16}{5}$;
∴$|AB|=\frac{32}{5}$;
(2)若存在斜率,设该直线方程为y=k(x-3),带入椭圆方程得:
(25k2+16)x2-150k2x+225k2-400=0;
设A(x1,y1),B(x2,y2);
∴${x}_{1}+{x}_{2}=\frac{150{k}^{2}}{25{k}^{2}+16}$,${x}_{1}{x}_{2}=\frac{225{k}^{2}-400}{25{k}^{2}+16}$;
∴$|AB|=\sqrt{1+{k}^{2}}•\sqrt{({x}_{1}+{x}_{2})^{2}-4{x}_{1}{x}_{2}}$=$\frac{160(1+{k}^{2})}{25{k}^{2}+16}$=$\frac{32}{5}+\frac{288}{5(25{k}^{2}+16)}$;
25k2+16≥16;
$0<\frac{1}{5(25{k}^{2}+16)}≤\frac{1}{80}$;
∴$\frac{32}{5}<|AB|≤10$;
∴综上得,$\frac{32}{5}≤|AB|≤10$;
∴|AB|的最大值为10,最小值为$\frac{32}{5}$.
点评 考查直线的点斜式方程,椭圆的标准方程,椭圆的焦点,弦及弦长的概念,以及弦长公式,韦达定理,根据不等式的性质求函数值域的方法.

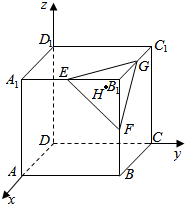 如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.
如图,在空间直角坐标系中有一棱长为m的正方体ABCD-A1B1C1D1,E,F,G,分别为A1B1,B1C1,BB1的中点,H为△EFG的重心,求DH的长度.