题目内容
14.方程x${\;}^{\frac{2}{5}}$=|x2-1|在实数集上的解的个数有4.分析 方程x${\;}^{\frac{2}{5}}$=|x2-1|在实数集上的解的个数可化为函数y=x${\;}^{\frac{2}{5}}$与y=|x2-1|的图象的交点的个数,作图求解即可.
解答 解:作函数y=x${\;}^{\frac{2}{5}}$与y=|x2-1|的图象如下,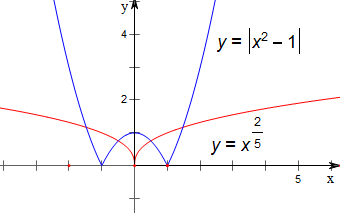
由图象可知,函数y=x${\;}^{\frac{2}{5}}$与y=|x2-1|的图象有四个交点,
故方程x${\;}^{\frac{2}{5}}$=|x2-1|在实数集上的解的个数为4.
故答案为:4.
点评 本题考查了数形结合的应用及方程的根与函数的图象的交点的关系应用,属于中档题.

练习册系列答案
相关题目
 已知抛物线M:y2=2px(p>0),其焦点F到直线l:x-y-2t=0的距离为$\frac{3\sqrt{2}}{2}$.
已知抛物线M:y2=2px(p>0),其焦点F到直线l:x-y-2t=0的距离为$\frac{3\sqrt{2}}{2}$.