题目内容
(本小题满分13分)
已知数列{an}的首项a1=" t" >0, ,n=1,2,……
,n=1,2,……
(1)若t = ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式;
(2)若 对一切
对一切 都成立,求t的取值范围.
都成立,求t的取值范围.
(1)将所给关系式取导数,即得递推关系式,从而得证,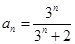 (2)0<t<1
(2)0<t<1
解析试题分析:(1)由题意 ,
, ,
,
所以 ,又因为
,又因为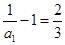 , ……4分
, ……4分
所以数列{ }是首项为
}是首项为 ,公比为
,公比为 的等比数列, ……5分
的等比数列, ……5分
根据等比数列的通项公式得 ,
,
所以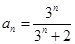 . ……7分
. ……7分
(2)由(1)知 ,
,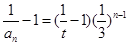 , ……9分
, ……9分
由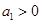 ,
, 知
知 ,故由
,故由 得
得 , ……10分
, ……10分
即( -1)(
-1)( )
) +1<(
+1<( -1)(
-1)( )
)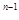 +1得
+1得 -1>0,
-1>0,
又t>0,则0<t<1. ……13分
考点:本小题主要考查由数列的递推关系式求数列的通项公式、等比数列的判定和通项公式的求解,以及恒成立问题的解决.
点评:由数列的递推关系式求数列的通项公式有累加法、累乘法和构造新数列法,要根据递推关系式的形式恰当选择.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 中,
中,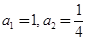 ,且
,且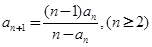 .
.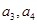 ,猜想
,猜想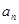 的表达式,并加以证明;
的表达式,并加以证明;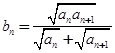 ,求证:对任意的自然数
,求证:对任意的自然数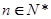 ,都有
,都有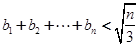 ;
; ,点
,点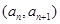 在函数
在函数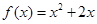 的图象上,其中
的图象上,其中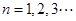
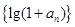 是等比数列;
是等比数列;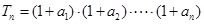 ,求
,求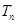 及数列
及数列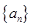 的通项;
的通项;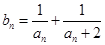 ,求数列
,求数列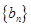 的前
的前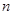 项和
项和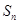 。
。 的前n项和为Sn=2n2,
的前n项和为Sn=2n2, 为等比数列,且
为等比数列,且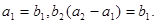
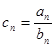 ,求数列
,求数列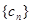 前n项和Tn.
前n项和Tn.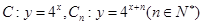 ,从
,从 上的点
上的点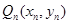 作
作 轴的垂线,交
轴的垂线,交 于点
于点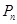 ,再从点
,再从点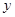 轴的垂线,交
轴的垂线,交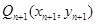 ,
,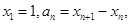
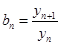 .。
.。 求数列
求数列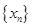 的通项公式;
的通项公式;  记
记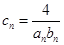 ,数列
,数列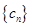 的前
的前 项和为
项和为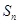 ,试比较
,试比较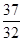 的大小
的大小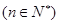 ;
; 记
记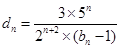 ,数列
,数列 的前
的前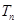 ,试证明:
,试证明: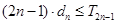 。
。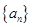 满足
满足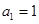 ,
,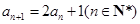 .
.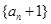 是等比数列,并写出数列
是等比数列,并写出数列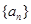 的通项公式;
的通项公式;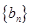 满足
满足 ,求
,求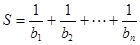 的值.
的值.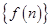 的前n项和为
的前n项和为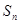 ,且
,且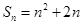 .
.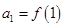 ,
,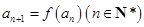 ,求证数列
,求证数列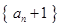 是等比数列,并求数
是等比数列,并求数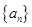 的前
的前 项和
项和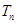 .
. 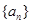 和
和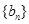 满足:
满足: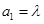 ,
,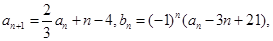 其中
其中 为实数,
为实数,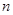 为正整数.
为正整数.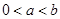 ,
,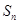 为数列
为数列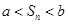 ?若存在,求
?若存在,求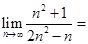 ___________.
___________.