题目内容
(本小题满分12分) 已知曲线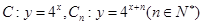 ,从
,从 上的点
上的点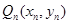 作
作 轴的垂线,交
轴的垂线,交 于点
于点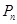 ,再从点
,再从点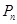 作
作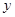 轴的垂线,交
轴的垂线,交 于点
于点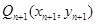 ,
,
设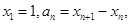
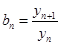 .。
.。 求数列
求数列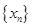 的通项公式;
的通项公式;  记
记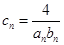 ,数列
,数列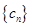 的前
的前 项和为
项和为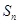 ,试比较
,试比较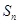 与
与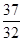 的大小
的大小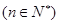 ;
;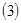 记
记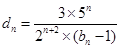 ,数列
,数列 的前
的前 项和为
项和为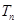 ,试证明:
,试证明: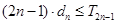 。
。


 ;
;
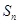 <
<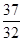 ;(3)
;(3)
解析试题分析:(1)依题意点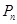 的坐标为
的坐标为 ,
, ,
, ,
,

 ;
;
(2)由(1)知,
 ,由
,由 ,
, ,
, ,
, 当
当 时,
时,


 ;.
;.
(3)当 时,有:
时,有:



 ,
,
又 ,
, ,
, .
.
所以对任意的 ,都有
,都有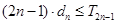 .
.
考点:数列的性质;数列通项公式的求法;数列前n项和的求法。
点评:若已知递推公式为 的形式求通项公式常用累加法。
的形式求通项公式常用累加法。
注:①若 是关于n的一次函数,累加后可转化为等差数列求和;
是关于n的一次函数,累加后可转化为等差数列求和;
②若 是关于n的二次函数,累加后可分组求和;
是关于n的二次函数,累加后可分组求和;
③ 是关于n的指数函数,累加后可转化为等比数列求和;
是关于n的指数函数,累加后可转化为等比数列求和;
④ 是关于n的分式函数,累加后可裂项求和。
是关于n的分式函数,累加后可裂项求和。

练习册系列答案
相关题目
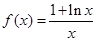 .
.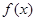 在区间
在区间 上有极值,求实数
上有极值,求实数 的取值范围;
的取值范围; 的方程
的方程 有实数解,求实数
有实数解,求实数 的取值范围;
的取值范围; ,
, 时,求证:
时,求证: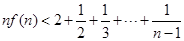 .
. 的首项为
的首项为 ,
, 时,
时, ,数列
,数列 对任意
对任意 均有
均有
 ,数列
,数列 满足
满足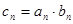 ,记数列
,记数列 项和为
项和为 ,求证
,求证 .
. ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数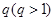 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项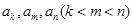 .
.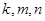 之间满足的等量关系;
之间满足的等量关系; 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确; 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.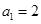 ,点
,点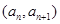 在函数
在函数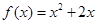 的图象上,其中
的图象上,其中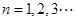
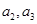 ;
;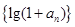 是等比数列;
是等比数列;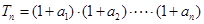 ,求
,求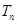 及数列
及数列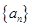 的通项
的通项 ,n=1,2,……
,n=1,2,…… ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式; 对一切
对一切 都成立,求t的取值范围.
都成立,求t的取值范围. 的前
的前 项和为
项和为 ,
, ,
, ,等差数列
,等差数列 满足
满足 ,
, ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的首项
的首项 ,
,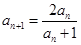 ,
,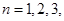 ….
….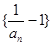 是等比数列;
是等比数列; 的前
的前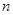 项和
项和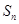 .
.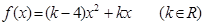 ,对任意实数
,对任意实数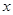 ,
,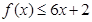 恒成立;正数数列
恒成立;正数数列 满足
满足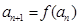 .
.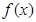 的解析式和值域;
的解析式和值域;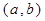 ,使得当
,使得当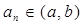 时,数列
时,数列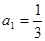 ,求证:数列
,求证:数列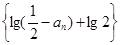 是等比数列
是等比数列