题目内容
(本小题满分14分)
已知数列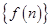 的前n项和为
的前n项和为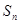 ,且
,且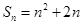 .
.
(Ⅰ)求数列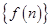 通项公式;
通项公式;
(Ⅱ)若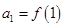 ,
,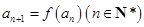 ,求证数列
,求证数列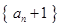 是等比数列,并求数
是等比数列,并求数
列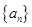 的前
的前 项和
项和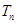 .
.
(Ⅰ)f(n)=2n+1(Ⅱ)证明见解析 
解析试题分析:(Ⅰ) 时,
时, ;
; 时,
时, ,
,
综上可得数列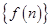 的通项为
的通项为
(Ⅱ) ,
, ,
, 又
又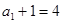
 是等比数列,首项为4,公比为2,
是等比数列,首项为4,公比为2,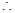 通项是
通项是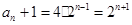 ,
,
数列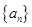 的前
的前 项和
项和
考点:数列求通项求和
点评:由 求
求 ,
, 时单独考虑,分组求和是求数列前
时单独考虑,分组求和是求数列前 项和的常用解法
项和的常用解法

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目
 中,
中, 且
且 成等差数列,
成等差数列, 成等比数列
成等比数列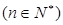
 及
及 ;
; ,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数
,从中选取若干项,不改变它们在原来数列中的先后次序,得到的数列称为是原来数列的一个子数列. 某同学在学习了这一个概念之后,打算研究首项为正整数 ,公比为正整数
,公比为正整数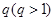 的无穷等比数列
的无穷等比数列 的子数列问题. 为此,他任取了其中三项
的子数列问题. 为此,他任取了其中三项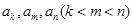 .
.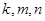 之间满足的等量关系;
之间满足的等量关系; 是等差数列”,为此,他研究了
是等差数列”,为此,他研究了 与
与 的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确;
的大小关系,请你根据该同学的研究结果来判断上述猜想是否正确; 的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明.
的无穷等差数列中是否存在成等比数列的子数列?请你就此问题写出一个正确命题,并加以证明. ,n=1,2,……
,n=1,2,…… ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式; 对一切
对一切 都成立,求t的取值范围.
都成立,求t的取值范围. 的前
的前 项和为
项和为 ,
, ,
, ,等差数列
,等差数列 满足
满足 ,
, ,
, 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.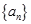 的前n项和为
的前n项和为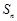 ,且满足
,且满足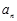 ,
,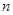 =1,2,3,….
=1,2,3,….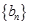 满足
满足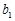 =1,且
=1,且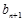 =
=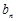 +
+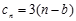 ,求数列
,求数列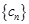 的前
的前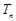 .
. 的首项
的首项 ,
,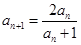 ,
,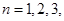 ….
….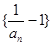 是等比数列;
是等比数列; 的前
的前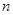 项和
项和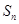 .
.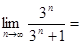 .
. }的前n项和
}的前n项和 ,
, |}的前n项和
|}的前n项和 .
.