题目内容
(本小题满分12分)已知数列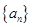 满足
满足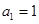 ,
,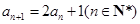 .
.
⑴求证:数列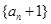 是等比数列,并写出数列
是等比数列,并写出数列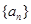 的通项公式;
的通项公式;
⑵若数列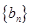 满足
满足 ,求
,求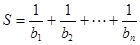 的值.
的值.
(1)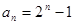 ,证明见解析(2)
,证明见解析(2)
解析试题分析:(1) ,
, ,
,
又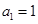 ,∴
,∴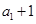 ≠0,
≠0, ≠0,∴
≠0,∴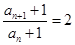 ,
,
∴数列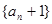 是首项为2,公比为2的等比数列.
是首项为2,公比为2的等比数列.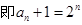 ,因此
,因此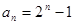 . ……6分
. ……6分
(2)∵ ,∴
,∴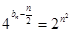 ,
,
∴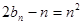 , 即
, 即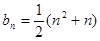 .
. 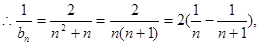
∴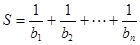
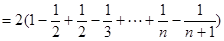
 . ……12分
. ……12分
考点:本小题主要考查构造法证明等比数列以及等比数列通项公式的求法以及裂项相消法求数列的前n项和,考查学生的转化能力和运算求解能力.
点评:构造法求数列的通项公式是常考的一种方法,利用时要注意是否取到了第一项,如果没有取到,则需要再验证第一项;裂项相消法和错位相减法是求数列的前n项和的重要方法,裂项相消法难度不大,但首先要保证正确裂项.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
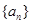 为等比数列,
为等比数列,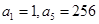 ;
;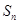 为等差数列
为等差数列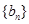 的前n项和,
的前n项和,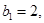
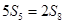 .
.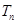
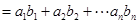 ,求
,求 的前
的前 项和为
项和为 .已知
.已知 ,
,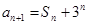 ,
, .
. ,求数列
,求数列 的通项公式;
的通项公式; ,
, ,求
,求 的取值范围.
的取值范围.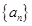 前
前 项和为
项和为 ,
,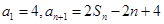 .
. 为等比数列;
为等比数列;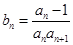 ,数列
,数列 前
前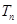 ,求证:
,求证: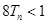 .
. ,n=1,2,……
,n=1,2,…… ,求
,求 是等比数列,并求出{an}的通项公式;
是等比数列,并求出{an}的通项公式; 对一切
对一切 都成立,求t的取值范围.
都成立,求t的取值范围.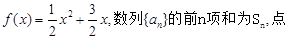
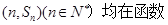
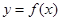
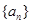 的通项公式
的通项公式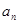 ;
; 求数列
求数列
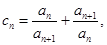 证明:
证明: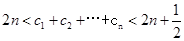 。
。 的前n项和为
的前n项和为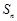 ,且满足
,且满足 ,
,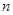 =1,2,3,….
=1,2,3,….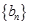 满足
满足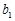 =1,且
=1,且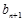 =
=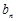 +
+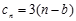 ,求数列
,求数列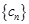 的前
的前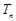 .
.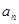 }中,
}中,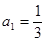 ,并且对任意
,并且对任意 都有
都有 成立,令
成立,令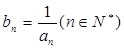 .
. }的通项公式;
}的通项公式;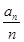 }的前n项和为
}的前n项和为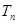 ,证明:
,证明:
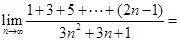 .
.