题目内容
5.已知|$\overrightarrow{a}$|=|$\overrightarrow{b}$|=1,向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为120°,且($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$+t$\overrightarrow{b}$),则实数t的值为( )| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
分析 利用向量垂直得到数量积为0,由此得到关于t的等式解之.
解答 解:由已知得到$\overrightarrow{a}•\overrightarrow{b}=|\overrightarrow{a}||\overrightarrow{b}|cos120°$=-$\frac{1}{2}$,
由($\overrightarrow{a}$+$\overrightarrow{b}$)⊥($\overrightarrow{a}$+t$\overrightarrow{b}$),则($\overrightarrow{a}$+$\overrightarrow{b}$)•($\overrightarrow{a}$+t$\overrightarrow{b}$)=0,则${\overrightarrow{a}}^{2}+t{\overrightarrow{b}}^{2}+(t+1)\overrightarrow{a}•\overrightarrow{b}$=0,
所以1+t-$\frac{1}{2}$(t+1)=0,解得t=-1;
故选:B.
点评 本题考查了平面向量的数量积公式的运用以及向量垂直的性质运用;属于基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.设变量x,y满足约束条件$\left\{\begin{array}{l}{x≥0}\\{x+y-4≤0}\\{x-3y+4≤0}\end{array}\right.$,则目标函数Z=x-y的最大值为( )
| A. | 4 | B. | 1 | C. | 0 | D. | -$\frac{4}{3}$ |
20.设m,n表示两条不同直线,α,β表示两个不同的平面,下列说法正确的是( )
| A. | 若m∥β,β⊥α则m⊥α | B. | 若m⊥n,n⊥β,β⊥α,则m⊥α | ||
| C. | 若m⊥α,m⊥n则n∥α | D. | 若m⊥α,n?α,则m⊥n |
13.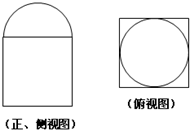 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
 如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )
如图是某几何体的三视图(正视图与侧视图一样,上面是半径为1的半圆,下面是边长为2的正方形),则该几何体的体积是( )| A. | 8+$\frac{2}{3}$π | B. | 8+$\frac{4}{3}$π | C. | 24+π | D. | 20+2π |
14.若不等式(-1)na<2+$\frac{(-1)^{n+1}}{n}$对于任意正整数n都成立,则实数a的取值范围是( )
| A. | $[-2,\frac{3}{2})$ | B. | $(-2,\frac{3}{2}]$ | C. | [-3,2] | D. | (-3,1) |
 如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率:
如图,在等腰三角形ABC中,∠B=∠C=30°,求下列事件的概率: