题目内容
【题目】已知一圆经过点![]() ,
,![]() ,且它的圆心在直线
,且它的圆心在直线![]() 上.
上.
(I)求此圆的方程;
(II)若点![]() 为所求圆上任意一点,且点
为所求圆上任意一点,且点![]() ,求线段
,求线段![]() 的中点
的中点![]() 的轨迹方程.
的轨迹方程.
【答案】(I)![]() ;(II)
;(II)![]() .
.
【解析】
试题分析:(I)方法一:由已知可设圆心![]()
![]()
![]()
![]()
![]()
![]() 圆心
圆心![]() ,
,![]()
![]()
![]() 圆
圆![]() 的方程为
的方程为![]() .方法二:由
.方法二:由![]() ,
,![]()
![]()
![]()
![]() 线段
线段![]() 的中点坐标为
的中点坐标为![]()
![]()
![]() 的垂直平分线方程为
的垂直平分线方程为![]() 即
即![]()
![]() 方程组
方程组![]()
![]()
![]()
![]() 圆心
圆心![]()
![]()
![]()
![]() 圆
圆![]() 的方程为
的方程为![]() ;(II)设
;(II)设![]() ,
,![]()
![]()
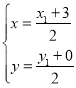
![]()
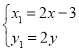
![]()
![]()
![]()
![]() .
.
试题解析:(I)方法一:由已知可设圆心![]()
![]() ,又由已知得
,又由已知得![]() ,从而有
,从而有
![]() ,解得:
,解得:![]() .
.
于是圆![]() 的圆心
的圆心![]() ,半径
,半径![]() .
.
所以,圆![]() 的方程为
的方程为![]() .
.
方法二:∵![]() ,
,![]() ,∴
,∴![]() ,线段
,线段![]() 的中点坐标为
的中点坐标为![]()
从而线段![]() 的垂直平分线的斜率为
的垂直平分线的斜率为![]() ,方程为
,方程为![]() 即
即![]()
由方程组![]() 解得
解得![]() ,
,
所以圆心![]() ,半径
,半径![]() ,
,
故所求圆N的方程为![]()
(II)设![]() ,
,![]() ,则由
,则由![]() 及
及![]() 为线段
为线段![]() 的中点得:
的中点得:
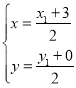 解得:
解得: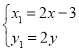 .
.
又点![]() 在圆
在圆![]() 上,所以有
上,所以有![]() ,化简得:
,化简得:![]() .
.
故所求的轨迹方程为![]()

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
【题目】某校高三共有2000名学生参加广安市联考,现随机抽取100名学生的成绩(单位:分),并列成如下表所示的频数分布表:
组别 |
|
|
|
|
|
|
频数 | 6 | 18 | 28 | 26 | 17 | 5 |
(1)试估计该年级成绩![]() 分的学生人数;
分的学生人数;
(2)已知样本中成绩在![]() 中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
中的6名学生中,有4名男生,2名女生,现从中选2人进行调研,求恰好选中一名男生一名女生的概率.
