题目内容
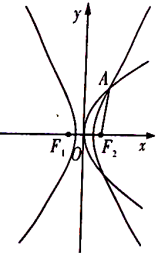
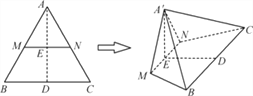
【题目】如图1,在高为2的梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,过
,过![]() 、
、![]() 分别作
分别作![]() ,
, ![]() ,垂足分别为
,垂足分别为![]() 、
、![]() 。已知
。已知![]() ,将梯形
,将梯形![]() 沿
沿![]() 、
、![]() 同侧折起,得空间几何体
同侧折起,得空间几何体![]() ,如图2。
,如图2。

(1)若![]() ,证明:
,证明: ![]() ;
;
(2)若![]() ,证明:
,证明: ![]() ;
;
(3)在(1),(2)的条件下,求三棱锥![]() 的体积。
的体积。
【答案】(1)见解析;(2)见解析;(3)![]() .
.
【解析】试题分析:
(1)由题意可得![]() ,则
,则![]() ,即
,即![]() 为直角三角形;
为直角三角形;
(2)利用题意可得![]() ,结合线面平行的判断定理可得
,结合线面平行的判断定理可得![]() ;
;
(3)利用题意可得AE为三棱锥的高,结合体积公式可得![]() .
.
试题解析:
(1)证明:由已知得,四边形![]() 为正方形,且边长为2,则在图2中,
为正方形,且边长为2,则在图2中, ![]()
由已知![]() ,
, ![]() ,可得
,可得![]() ,
,
又![]() ,所以
,所以![]() ,
,
又![]() ,
, ![]() ,所以
,所以![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() 。
。
(2)证明:如图,取AC的中点G,连接OG,DG,则![]() ,
,
则四边形DEOG为平行四边形,所以![]() ,
,
又![]() ,
, ![]() ,所以
,所以![]() 。
。
(3)解:因为三棱锥![]() 的体积
的体积![]() ,
,
而![]() ,
, ![]() ,所以
,所以![]() 。
。
即![]()
故![]()

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某工厂为了对新研发的产品进行合理定价,将该产品按事先拟定的价格进行试销,得到一组检测数据![]() (
(![]() …
…![]() )如下表所示:
)如下表所示:
试销价格
| 4 | 5 | 6 | 7 |
| 9 |
产品销量
|
| 84 | 83 | 80 | 75 | 68 |
已知变量![]() 具有线性负相关关系,且
具有线性负相关关系,且![]() ,
,![]() ,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲
,现有甲、乙、丙三位同学通过计算求得其回归直线方程分别为:甲![]() ,乙
,乙![]() ,丙
,丙![]() ,其中有且仅有一位同学的计算结果是正确的( ).
,其中有且仅有一位同学的计算结果是正确的( ).
(1)试判断谁的计算结果正确?并求出![]() 的值;
的值;
(2)若由线性回归方程得到的估计数据与检测数据的误差不超过1,则该检测数据是“理想数据”,现从检测数据中随机抽取2个,![]() 为“理想数据”的个数,求随机变量
为“理想数据”的个数,求随机变量![]() 的分布列和数学期望.
的分布列和数学期望.