题目内容
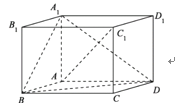
【题目】如图所示,直角梯形![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 上的点,且
上的点,且![]() ,
,![]() .沿
.沿![]() 将四边形
将四边形![]() 翻折至
翻折至![]() ,连接
,连接![]() 、
、![]() 、
、![]() ,得到多面体
,得到多面体![]() ,且
,且![]() .
.
(Ⅰ)求多面体![]() 的体积;
的体积;
(Ⅱ)求证:平面![]() ⊥平面
⊥平面![]() .
.
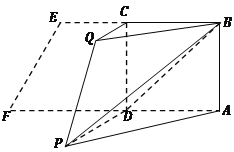
【答案】(Ⅰ)![]() ;(Ⅱ)证明见解析.
;(Ⅱ)证明见解析.
【解析】试题分析:
(Ⅰ)根据勾股定理的逆定理可得![]() ,进而可得
,进而可得![]() ⊥平面
⊥平面![]() ,故得平面
,故得平面![]() ⊥平面
⊥平面![]() ,根据面面垂直的性质得
,根据面面垂直的性质得![]() ⊥平面
⊥平面![]() ,将多面体
,将多面体![]() 的体积分为
的体积分为![]() 两部分求解.(Ⅱ)取
两部分求解.(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .根据等腰三角形性质得
.根据等腰三角形性质得![]() ,同理可得
,同理可得![]() ,故可得
,故可得![]() ⊥平面
⊥平面![]() ,从而平面
,从而平面![]() ⊥平面
⊥平面![]() .
.
试题解析:
(Ⅰ)依题意,![]() ,
,
∴![]() .
.
又![]() ,
,![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.
又平面![]() 平面
平面![]() ,
,![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
∴![]()
![]() .
.
(Ⅱ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() 、
、![]() .
.
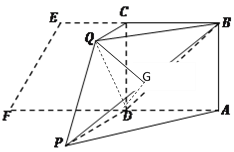
在△![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
又点![]() 为
为![]() 的中点,
的中点,
所以![]()
∴![]() ,
,
同理,在△![]() 中,
中,![]() ,
,![]() ,
,
又![]() ,
,
∴![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() ⊥平面
⊥平面![]() ,
,
∵![]() 平面
平面![]() ,
,
∴平面![]() ⊥平面
⊥平面![]() .
.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案【题目】某百货商店今年春节期间举行促销活动,规定消费达到一定标准的顾客可进行一次抽奖活动,随着抽奖活动的有效开展,参与抽奖活动的人数越来越多,该商店经理对春节前![]() 天参加抽奖活动的人数进行统计,
天参加抽奖活动的人数进行统计,![]() 表示第
表示第![]() 天参加抽奖活动的人数,得到统计表格如下:
天参加抽奖活动的人数,得到统计表格如下:
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 5 | 8 | 8 | 10 | 14 | 15 | 17 |
(Ⅰ)经过进一步统计分析,发现![]() 与
与![]() 具有线性相关关系.请根据上表提供的数据,用最小二乘法求出
具有线性相关关系.请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(Ⅱ)该商店规定:若抽中“一等奖”,可领取![]() 元购物券;抽中“二等奖”可领取
元购物券;抽中“二等奖”可领取![]() 元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为
元购物券;抽中“谢谢惠顾”,则没有购物券.已知一次抽奖活动获得“一等奖”的概率为![]() ,获得“二等”的概率为
,获得“二等”的概率为![]() .现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额
.现有张、王两位先生参与了本次活动,且他们是否中奖相互独立,求此二人所获购物券总金额![]() 的分布列及数学期望.
的分布列及数学期望.
参考公式: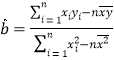 ,
,![]() ,
,![]() .
.
【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.