题目内容
【题目】(2017安徽蚌埠一模)已知椭圆C:![]() =1(a>b>0)的离心率为
=1(a>b>0)的离心率为![]() ,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2
,F1,F2是椭圆的两个焦点,P是椭圆上任意一点,且△PF1F2的周长是8+2![]() .
.

(1)求椭圆C的方程;
(2)设圆T:(x-2)2+y2=![]() ,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
,过椭圆的上顶点M作圆T的两条切线交椭圆于E,F两点,求直线EF的斜率.
【答案】(1)![]() +y2=1. (2)
+y2=1. (2)![]() .
.
【解析】试题分析:
(1)由椭圆的离心率为![]() 可得a=4b,c=
可得a=4b,c=![]() b,然后根据△PF1F2的周长可得b=1,a=4,从而可得椭圆的方程.(2)由题意知过点M与圆T相切的直线存在斜率,设其方程为y=kx+1,由直线与圆相切可得32k2+36k+5=0,从而得到
b,然后根据△PF1F2的周长可得b=1,a=4,从而可得椭圆的方程.(2)由题意知过点M与圆T相切的直线存在斜率,设其方程为y=kx+1,由直线与圆相切可得32k2+36k+5=0,从而得到![]() ,
,![]() .然后分别求出两切线与椭圆交点的横坐标
.然后分别求出两切线与椭圆交点的横坐标![]() 和
和![]() ,最后根据斜率公式求解即可.
,最后根据斜率公式求解即可.
试题解析:
(1)由题意得e=![]() ,
,
∴a=4b,
∴c=![]() b.
b.
∵△PF1F2的周长是8+2![]() ,
,
∴2a+2c=![]() 8+2
8+2![]() ,
,
∴b=1,
∴a=4.
∴椭圆C的方程为![]() +y2=1.
+y2=1.
(2)由(1)得椭圆的上顶点为M(0,1),
又由题意知过点M与圆T相切的直线存在斜率,设其方程为l:y=kx+1,
∵直线y=kx+1与圆T相切,
∴![]() ,
,
整理得32k2+36k+5=0,
∴![]()
由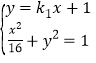 消去y整理得(1+16
消去y整理得(1+16![]() )x2+32k1x=0,
)x2+32k1x=0,
∴![]() .
.
同理可得![]() ,
,
∴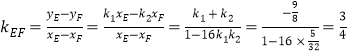 .
.
故直线EF的斜率为![]() .
.

【题目】随着社会的发展,终身学习成为必要,工人知识要更新,学习培训必不可少,现某工厂有工人1000名,其中250名工人参加短期培训(称为![]() 类工人),另外750名工人参加过长期培训(称为
类工人),另外750名工人参加过长期培训(称为![]() 类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到
类工人),从该工厂的工人中共抽查了100名工人,调查他们的生产能力(此处生产能力指一天加工的零件数)得到![]() 类工人生产能力的茎叶图(左图),
类工人生产能力的茎叶图(左图),![]() 类工人生产能力的频率分布直方图(右图).
类工人生产能力的频率分布直方图(右图).

(1)问![]() 类、
类、![]() 类工人各抽查了多少工人,并求出直方图中的
类工人各抽查了多少工人,并求出直方图中的![]() ;
;
(2)求![]() 类工人生产能力的中位数,并估计
类工人生产能力的中位数,并估计![]() 类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
类工人生产能力的平均数(同一组中的数据用该组区间的中点值作代表);
(3)若规定生产能力在![]() 内为能力优秀,由以上统计数据在答题卡上完成下面的
内为能力优秀,由以上统计数据在答题卡上完成下面的![]() 列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
列联表,并判断是否可以在犯错误概率不超过0.1%的前提下,认为生产能力与培训时间长短有关.能力与培训时间列联表
短期培训 | 长期培训 | 合计 | |
能力优秀 | |||
能力不优秀 | |||
合计 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() ,其中
,其中![]() .
.