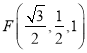题目内容
【题目】如图,已知椭圆![]() :
: ![]() ,其左右焦点为
,其左右焦点为![]() 、
、![]() ,过点
,过点![]() 的直线交椭圆
的直线交椭圆![]() 于
于![]() ,
, ![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
, ![]() 的中垂线与
的中垂线与![]() 轴和
轴和![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,且
两点,且![]() 、
、![]() 、
、![]() 构成等差数列.
构成等差数列.

(1)求椭圆![]() 的方程;
的方程;
(2)记![]() 的面积为
的面积为![]() ,
, ![]() (
(![]() 为原点)的面积为
为原点)的面积为![]() ,试问:是否存在直线
,试问:是否存在直线![]() ,使得
,使得![]() ?说明理由.
?说明理由.
【答案】(1)椭圆![]() 的方程为
的方程为![]() ;(2)方程为
;(2)方程为![]() .
.
【解析】试题分析:(1)第一问比较简单直接列一个方程组,解出a,b,c即可. (2)第二问首先需要设出直线的方程![]() (
(![]() ),再利用
),再利用![]() 和相似得到
和相似得到![]() ,化简这个方程需要点G和点D的坐标,利用韦达定理求出点G和点D的坐标代入
,化简这个方程需要点G和点D的坐标,利用韦达定理求出点G和点D的坐标代入![]() 解关于k的方程即可.
解关于k的方程即可.
试题解析:(1)因为![]() 、
、![]() 、
、![]() 构成等差数列,
构成等差数列,
所以![]() ,所以
,所以![]() ,
,
又因为![]() ,所以
,所以![]() ,
,
所以椭圆![]() 的方程为
的方程为![]() .
.
(2)假设存在直线![]() ,使得
,使得![]() ,显然直线
,显然直线![]() 不能与
不能与![]() ,
, ![]() 轴垂直.
轴垂直.
设![]() 方程为
方程为![]() (
(![]() ),
),
将其代入![]() ,整理得
,整理得![]() ,
,
设![]() ,
, ![]() ,所以
,所以![]() ,
,
故点![]() 的横坐标为
的横坐标为![]() ,所以
,所以 ,
,
设![]() ,因为
,因为![]() ,所以
,所以 ,
,
解得![]() ,即
,即 .
.
∵![]() 和
和![]() 相似,且
相似,且![]() ,则
,则![]() ,,
,,
∴ ,
,
整理得![]() ,因此
,因此![]() ,
, ![]() ,
,
所以存在直线![]() ,方程为
,方程为![]() .
.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目