Question

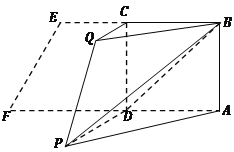
【题目】在平行六面体中，平面，且 ，．

（1）求异面直线与所成角的余弦值；

（2）求二面角的正弦值．

Answer 1

【答案】（1）；（2）.

【解析】试题分析：在平面内，过点作，因为平面，可得，以为坐标原点，分别以所在直线为轴建立空间直角坐标系，结合平行六面体的性质求出的坐标，进一步求出 的坐标 ，（1）直接利用空间向量向量所成角的余弦公式可得异面直线与所成角的余弦值 ；（2）求出平面与平面的一个法向量，再根据空间向量夹角余弦公式求出两法向量所成角的余弦值求得二面角的余弦值，进一步得到正弦值.

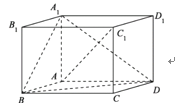
试题解析：在平面ABCD内，过点A作AEAD，交BC于点E．因为AA1平面ABCD，所以AA1AE，AA1AD．

如图，以为正交基底，建立空间直角坐标系A-xyz．因为AB=AD=2，AA1=，．

则．

（1），

则．异面直线A1B与AC1所成角的余弦值为．

(2)平面的一个法向量为，设为平面的一个法向量，又，则，即，不妨取，则为平面的一个法向量，从而，设二面角B-A1D-A的大小为，则．因为，所以．因此二面角B-A1D-A的正弦值为．

【方法点晴】本题主要考查利用空间向量求异面直线所成的角及二面角，属于难题.空间向量解答立体几何问题的一般步骤是：（1）观察图形，建立恰当的空间直角坐标系；（2）写出相应点的坐标，求出相应直线的方向向量；（3）设出相应平面的法向量，利用两直线垂直数量积为零列出方程组求出法向量；（4）将空间位置关系转化为向量关系；（5）根据定理结论求出相应的角和距离.