题目内容
【题目】设△AnBnCn的三边长分别为an ， bn ， cn ， △AnBnCn的面积为Sn ， n=1，2，3…若b1＞c1 ， b1+c1=2a1 ， an+1=an ， 
， 
，则（ ）
A.{Sn}为递减数列
B.{Sn}为递增数列
C.{S2n﹣1}为递增数列，{S2n}为递减数列
D.{S2n﹣1}为递减数列，{S2n}为递增数列
【答案】B
【解析】解：b1=2a1﹣c1且b1＞c1 ， ∴2a1﹣c1＞c1 ， ∴a1＞c1 ，
∴b1﹣a1=2a1﹣c1﹣a1=a1﹣c1＞0，∴b1＞a1＞c1 ，
又b1﹣c1＜a1 ， ∴2a1﹣c1﹣c1＜a1 ， ∴2c1＞a1 ， ∴ 
，
由题意， 
+an ， ∴bn+1+cn+1﹣2an= 
（bn+cn﹣2an），
∴bn+cn﹣2an=0，∴bn+cn=2an=2a1 ， ∴bn+cn=2a1 ，
又由题意，bn+1﹣cn+1= 
，∴ 
=a1﹣bn ，
∴bn+1﹣a1= 
，∴bn﹣a1= 
，
∴ 
，cn=2a1﹣bn= 
，
∴ 
[ 
][ 
]
= 
[ 
﹣ 
]单调递增（可证当n=1时 
＞0）
故选B．
【考点精析】解答此题的关键在于理解数列的通项公式的相关知识，掌握如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
【题目】某商店为了解气温对某产品销售量的影响，随机记录了该商店
月份中
天的日销售量
（单位：千克）与该地当日最低气温
（单位：℃）的数据，如表所示：
|
|
|
|
|
|
|
|
|
|
|
|
（1）求与的回归方程
：
（2）判断与之间是正相关还是负相关；若该地月份某天的最低气温为
，请用（1）中的回归方程预测该商店当日的销售量．
参考公式：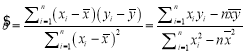
，
．
