题目内容
【题目】如图,矩形![]() 所在的半平面和直角梯形
所在的半平面和直角梯形![]() 所在的半平面成
所在的半平面成![]() 的二面角,
的二面角,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.

(Ⅰ)求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)试问在线段![]() 上是否存在一点
上是否存在一点![]() ,使锐二面角
,使锐二面角![]() 的余弦值为
的余弦值为![]() .若存在,请求出
.若存在,请求出![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(Ⅰ)见证明;(Ⅱ)见解析
【解析】
(Ⅰ)根据二面角的平面角的定义得到![]() 即为二面角
即为二面角![]() 的平面角
的平面角![]() ,根据
,根据![]() ,
,![]() 得到线面垂直,进而得到面面垂直;(Ⅱ)根据二面角的平面角的定义,结合三垂线法做出平面角
得到线面垂直,进而得到面面垂直;(Ⅱ)根据二面角的平面角的定义,结合三垂线法做出平面角![]() 是锐二面角
是锐二面角![]() 的平面角,由几何关系得到相应结果即可.
的平面角,由几何关系得到相应结果即可.
(Ⅰ)证明:∵![]() ,
,![]() ,
,
∴![]() 即为二面角
即为二面角![]() 的平面角,
的平面角,
∴![]() .
.
又∵![]() ,
,
∴![]() 平面
平面![]() ,
,
又∵![]() 平面
平面![]() ,
,
∴平面![]() 平面
平面![]() .
.
(Ⅱ)在线段![]() 上存在一点
上存在一点![]() ,当
,当![]() 符合题意,
符合题意,
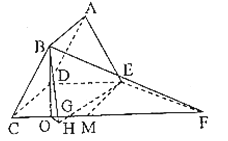
∵平面![]() 平面
平面![]() ,在平面
,在平面![]() 内,作
内,作![]() 于
于![]() ,
,
又∵平面![]() 平面
平面![]() ,则
,则![]() 平面
平面![]() .
.
过![]() 作
作![]() 于H,连接
于H,连接![]() ,∵
,∵![]() 为
为![]() 在平面
在平面![]() 的射影,
的射影,
∴![]() 是锐二面角
是锐二面角![]() 的平面角,
的平面角,
因为![]() ,又因为锐二面角
,又因为锐二面角![]() 的余弦值是
的余弦值是![]() ,
,
所以![]() .
.
取![]() 中点
中点![]() ,易知
,易知![]() 与
与![]() 相似,设
相似,设![]() ,则
,则![]() ,
,
即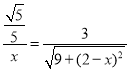 ,解得
,解得![]() 或
或![]() (舍),
(舍),
因此存在符合题意的点![]() ,使得
,使得![]() .
.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目