Question

【题目】已知函数

（1）若不等式的解集为，求实数的值；

（2）若不等式对一切实数恒成立，求实数的取值范围；

Answer 1

【答案】（1）（2）

【解析】分析：（1）根据二次不等式的解集与二次方程的根的关系可得参数；

（2）这个不等式恒成立，首先讨论时，能不能恒成立，其次在时，这是二次不等式，结合二次函数的性质可求解．

详解：（1）的解集为，则的解为和2，且，

∴，解得．

（2）由，得，

若a=0，不等式不对一切实数x恒成立，舍去，

若a≠0，由题意得，解得：，

故a的范围是：

判别式 Δ＝b2－4ac	Δ>0	Δ＝0	Δ<0
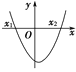
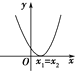
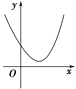
二次函数y＝ax2＋bx＋c (a>0)的图象
一元二次方程 ax2＋bx＋c＝0 (a>0)的根	有两相异实根 x1，x2(x1<x2)	有两相等实根 x1＝x2＝－	没有实数根
ax2＋bx＋c>0(a>0)的解集	{x|x<x1或x>x2}	{x|x≠x1}	R
ax2＋bx＋c<0(a>0)的解集	{x|x1<x<x2}