题目内容
【题目】(本题满分12分)已知函数f(x)=ex, g(x)=lnx.
(1)设f(x)在x1处的切线为l1, g(x)在x2处的切线为l2,若l1//l2,求x1+g(x2)的值;
(2)若方程af 2(x)-f(x)-x=0有两个实根,求实数a的取值范围;
(3)设h(x)=f(x)(g(x)-b),若h(x)在[ln2,ln3]内单调递减,求实数b的取值范围.
【答案】(1)0.
(2) 0<a<1.
(3) b≥ln2+![]() .
.
【解析】分析:(1)求导,利用l1//l2时k值相等,即可求出答案;
(2)参变分离,利用导数的应用以及数形结合即可得到答案;
(3)由题意h(x)=f(x)(g(x)-b)=ex(lnx-b),求导,因为h(x)在[ln2,ln3]内单调递减,所以![]() 在[ln2,ln3]上恒成立,再参变分离,分析讨论即可.
在[ln2,ln3]上恒成立,再参变分离,分析讨论即可.
详解:(1) f′(x)=ex, g′(x)=![]()
由题意知:![]() =
=![]()
故x1+g(x2)=x1-ln![]() =0.
=0.
(2) 方程af 2(x)-f(x)-x=0,ae2x-ex-x=0,a=![]()
令φ(x)=![]() , 则φ′(x)=-
, 则φ′(x)=-![]()
当x<0时,ex<1,ex-1<0,所以ex+2x-1<0,所以φ′(x)>0,故φ(x)单调增;
当x>0时,ex>1,ex-1>0,所以ex+2x-1>0,所以φ′(x)<0,故φ(x)单调减.
从而φ(x)max=φ(0)=1
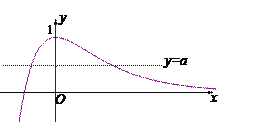
又,当x>0时,φ(x)=![]() >0
>0
原方程有两个实根等价于直线y=a与φ(x)的图像有两个交点,故0<a<1.
(3)由题意h(x)=f(x)(g(x)-b)=ex(lnx-b),得h′(x)=ex(lnx+![]() -b)
-b)
因为h(x)在[ln2,ln3]内单调递减,所以h′(x)=ex(lnx+![]() -b)≤0在[ln2,ln3]内恒成立
-b)≤0在[ln2,ln3]内恒成立
由于ex>0,故只需lnx+![]() -b≤0在[ln2,ln3]内恒成立
-b≤0在[ln2,ln3]内恒成立
即b≥lnx+![]() 在[ln2,ln3]内恒成立
在[ln2,ln3]内恒成立
令t(x)=lnx+![]() , t′(x)=
, t′(x)=![]() -
-![]() =
=![]()
当ln2≤x<1时,t′(x)<0,故t(x)单调减;
当1≤x≤ln3时,t′(x)>0,故t(x)单调增.
下面只要比较t(ln2)与t(ln3)的大小.
思路:[详细过程略]

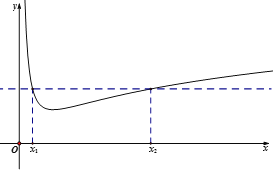
先证明:x1+x2>2
又,ln2+ln3=ln6<2
故当x1=ln2时,ln3< x2
即t(ln3)<t(ln2)
所以t(x)max=t(ln2)=ln2+![]()
所以b≥ln2+![]() .
.

 名校课堂系列答案
名校课堂系列答案【题目】高三年级有500名学生,为了了解数学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
分组 | 频数 | 频率 |
|
|
|
|
| |
|
| |
| 12 |
|
|
| |
| 4 |
|
|
| |
合计 |
|
![]() 根据上面图表,求
根据上面图表,求![]() 处的数值
处的数值
![]() 在所给的坐标系中画出
在所给的坐标系中画出![]() 的频率分布直方图;
的频率分布直方图;
![]() 根据题中信息估计总体平均数,并估计总体落在
根据题中信息估计总体平均数,并估计总体落在![]() 中的概率.
中的概率.


