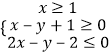Question

【题目】已知函数f(x)＝(x＋1)ln x－a(x－1)．

(1)当a＝4时，求曲线y＝f(x)在(1，f(1))处的切线方程；

(2)若当x∈(1，＋∞)时，f(x)>0恒成立，求a的取值范围．

Answer 1

【答案】（1）2x＋y－2＝0.（2）(－∞，2]．

【解析】试题分析：（1）根据导数几何意义得f′(1)＝k,再根据点斜式求切线方程（2）不等式恒成立问题一般转化为对应函数最值问题： ，利用导数可得函数单调性：为单调递增，再利用洛必达法则得，即得的取值范围

试题解析：解 (1)f(x)的定义域为(0，＋∞)．当a＝4时，

f(x)＝(x＋1)ln x－4(x－1)，f′(x)＝ln x＋－3，f′(1)＝－2，f(1)＝0.

故曲线y＝f(x)在(1，f(1))处的切线方程为2x＋y－2＝0.

(2)当x∈(1，＋∞)时，f(x)>0等价于ln x－>0.

设g(x)＝ln x－，则g′(x)＝－＝，g(1)＝0.

(i)当a≤2，x∈(1，＋∞)时，x2＋2(1－a)x＋1≥x2－2x＋1>0，故g′(x)>0，

g(x)在(1，＋∞)上单调递增，因此g(x)>0.

(ii)当a>2时，令g′(x)＝0，得x1＝a－1－，x2＝a－1＋.

由x2>1和x1x2＝1得x1<1，故当x∈(1，x2)时，g′(x)<0，g(x)在(1，x2)上单调递减，因此g(x)<0.

综上，a的取值范围是(－∞，2]．