题目内容

【题目】已知圆心（a，b）（a＜0，b＜0）在直线y=2x+1上的圆，若其圆心到x轴的距离恰好等于圆的半径，在y轴上截得的弦长为 ，则圆的方程为（ ）
A.（x+2）2+（y+3）2=9
B.（x+3）2+（y+5）2=25
C.
D.

【答案】A
【解析】解：根据题意画出图形，如图所示：
过M作MA⊥x轴，MB⊥y轴，连接MC，
由垂径定理得到B为CD中点，又|CD|=2 ，
∴|CB|= ，
由题意可知圆的半径|MA|=|MC|=|b|，|MB|=|a|，
在直角三角形BC中，根据勾股定理得：b2=a2+（ ）2 ， ①
又把圆心（a，b）代入y=2x+1中，得b=2a+1，②
联立①②，解得：a=﹣2，b=﹣3，
所以圆心坐标为（﹣2，﹣3），半径r=|﹣3|=3，
则所求圆的方程为：（x+2）2+（y+3）2=9．
故选A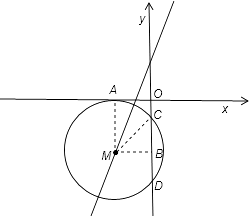

练习册系列答案
相关题目

【题目】已知函数f（x）=k﹣ （其中k为常数）；
（1）求：函数的定义域；
（2）证明：函数在区间（0，+∞）上为增函数；
（3）若函数为奇函数，求k的值．

【题目】如图，将一个各面都涂了油漆的正方体，切割为125个同样大小的小正方体，经过搅拌后，从中随机取一个小正方体，记它的涂漆面数为X，则X的均值E（X）=（ ）

A.
B.
C.
D.

【题目】如图，已知 =（2，1）， =（1，7）， =（5，1），设Z是直线OP上的一动点．

（1）求使 取最小值时的 ；
（2）对（1）中求出的点Z，求cos∠AZB的值．

【题目】已知函数f(x)＝(x＋1)ln x－a(x－1)．

(1)当a＝4时，求曲线y＝f(x)在(1，f(1))处的切线方程；

(2)若当x∈(1，＋∞)时，f(x)>0恒成立，求a的取值范围．

【题目】下列叙述正确的个数是（ ）
①若a＞b，则ac2＞bc2；
②若命题p为真命题题，命题q为假命题，则p∨q为假命题；
③若命题p：x0∈R，x ﹣x0+1≤0，则￢p：x∈R，x2﹣x+1＞0．
A.0
B.1
C.2
D.3

【题目】已知k∈R， =（k，1）， =（2，4），若| |＜ ，则△ABC是钝角三角形的概率是（ ）
A.
B.
C.
D.

【题目】已知抛物线E：x2=2py（p＞0），直线y=kx+2与E交于A、B两点，且 =2，其中O为原点．
（1）求抛物线E的方程；
（2）点C坐标为（0，﹣2），记直线CA、CB的斜率分别为k1 ， k2 ， 证明：k12+k22﹣2k2为定值．

【题目】已知△ABC的三个内角A，B，C所对的边分别是a，b，c，B是钝角，且 a=2bsinA．
（1）求B的大小；
（2）若△ABC的面积为 ，且b=7，求a+c的值；
（3）若b=6，求△ABC面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网