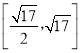Question

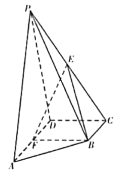
【题目】在如图的多面体中，EF⊥平面AEB，AE⊥EB，AD∥EF，EF∥BC，BC＝2AD＝4，EF＝3，AE＝BE＝2，G是BC的中点．

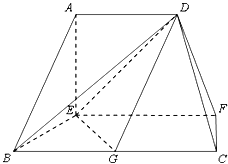
（Ⅰ）求证：AB∥平面DEG；

（Ⅱ）求证：BD⊥EG；

（Ⅲ）求多面体ADBEG的体积．

Answer 1

【答案】（Ⅰ）见解析（Ⅱ）见解析（Ⅲ）4

【解析】

（Ⅰ） 先证明四边形ADGB是平行四边形，可得AB∥DG，从而证明AB∥平面DEG．

（Ⅱ） 过D作DH∥AE交EF于H，则DH⊥平面BCFE，DH⊥EG，再证BH⊥EG，从而可证EG⊥平面BHD，故BD⊥EG．

（Ⅲ）要求多面体ADBEG的体积，利用分割的思想转化为VADBEG＝VD﹣AEB+VD﹣BEG转化为求两个三棱锥的体积即可．

（Ⅰ）∵AD∥EF，EF∥BC，∴AD∥BC．

又∵BC＝2AD，G是BC的中点，∴，∴四边形ADGB是平行四边形，∴AB∥DG，∵AB平面DEG，DG平面DEG，∴AB∥平面DEG．

（Ⅱ）∵EF⊥平面AEB，AE平面AEB，∴EF⊥AE，

又AE⊥EB，EB∩EF＝E，EB，EF平面BCFE，∴AE⊥平面BCFE．

过D作DH∥AE交EF于H，连接，则DH⊥平面BCFE．

∵EG平面BCFE，∴DH⊥EG．

∵AD∥EH，DH∥AE，∴四边形AEHD平行四边形，∴EH＝AD＝2，

∴EH＝BG＝2，又EH∥BG，EH⊥BE，

∴四边形BGHE为正方形，∴BH⊥EG，

又BH∩DH＝H，BH平面BHD，DH平面BHD，∴EG⊥平面BHD．

∵BD平面BHD，∴BD⊥EG．

（Ⅲ）∵EF⊥平面AEB，AD∥EF，∴AD⊥平面AEB，

由（2）知四边形BGHE为正方形，∴BE⊥BC．

∴VADBEG＝VD﹣AEB+VD﹣BEG4.