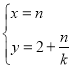题目内容
【题目】如图,已知抛物线![]() ,直线
,直线![]() 交抛物线于
交抛物线于![]() ,
,![]() 两点,
两点,![]() 是抛物线外一点,连接
是抛物线外一点,连接![]() ,
,![]() 分别交抛物线于点
分别交抛物线于点![]() ,
,![]() ,且
,且![]() .
.
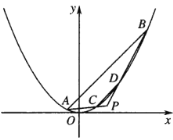
(Ⅰ)若![]() ,求点
,求点![]() 的轨迹方程;
的轨迹方程;
(Ⅱ)若![]() ,求
,求![]() 面积的最小值.
面积的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)联立直线与抛物线,利用韦达定理、定比分点坐标公式、导数的几何意义可求得点![]() 的横坐标为定值,再根据点
的横坐标为定值,再根据点![]() 在抛物线外可得点
在抛物线外可得点![]() 的纵坐标的范围,从而可得结果;
的纵坐标的范围,从而可得结果;
(Ⅱ)由(Ⅰ)和弦长公式求解.
(Ⅰ)设![]() ,
,![]() ,
,![]() ,
,
由![]() ,得
,得![]() ,
,
则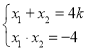 ,(*)
,(*)
因为![]() ,所以可设
,所以可设![]() ,
,![]() ,
,
所以由定比分点公式得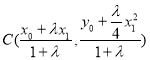 ,
,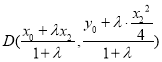 ,
,
将![]() 的坐标代入抛物线方程,得
的坐标代入抛物线方程,得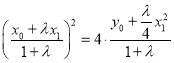 ,
,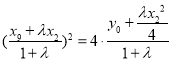 ,
,
化简得![]() ,
,
![]()
所以![]() 为方程
为方程![]() 的两根,
的两根,
联立(*)式得![]() ,
,
解得![]() .
.
设过抛物线上点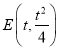 的切线与
的切线与![]() 平行,
平行,
因为![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]() ,
,![]() ,
,
所以点![]() 的轨迹方程为
的轨迹方程为![]() .
.
(Ⅱ)设![]() 的中点为
的中点为![]() ,
,
则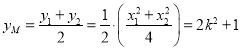 ,
,
由(Ⅰ)知![]() ,
,
因为![]() ,所以
,所以![]() ,
,
又![]() ,得
,得![]() ,
,
又![]()
![]() ,
,
所以![]()
![]() ,
,
显然当![]() 时,
时,![]() 取得最小值
取得最小值![]() .
.

练习册系列答案
相关题目
【题目】袋子中有四张卡片,分别写有“国”、“富”、“民”、“强”四个字,有放回地从中任取一张卡片,将三次抽取后“国”“富”两个字都取到记为事件A,用随机模拟的方法估计事件A发生的概率,利用电脑随机产生整数0,1,2,3四个随机数,分别代表“国”、“富”、“民”、“强”这四个字,以每三个随机数为一组,表示取卡片三次的结果,经随机模拟产生了以下18组随机数:
231 | 232 | 210 | 023 | 122 | 021 | 321 | 220 | 031 |
231 | 103 | 133 | 132 | 001 | 320 | 123 | 130 | 233 |
由此可以估计事件A发生的概率为_____.