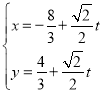题目内容
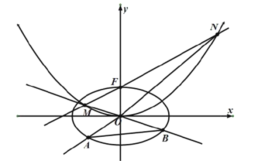
【题目】如图,已知椭圆![]() ,点
,点![]() 是抛物线
是抛物线![]() 的焦点,过点F作直线
的焦点,过点F作直线![]() 交抛物线于M,N两点,延长
交抛物线于M,N两点,延长![]() ,
,![]() 分别交椭圆于A,B两点,记
分别交椭圆于A,B两点,记![]() ,
,![]() 的面积分别是
的面积分别是![]() ,
,![]() .
.
(1)求![]() 的值及抛物线的准线方程;
的值及抛物线的准线方程;
(2)求![]() 的最小值及此时直线
的最小值及此时直线![]() 的方程.
的方程.
【答案】(1)![]() ,准线方程为
,准线方程为![]() ;(2)
;(2)![]() 的最小值是2,此时直线
的最小值是2,此时直线![]() 的方程是
的方程是![]() .
.
【解析】
(1)由焦点坐标得![]() 可得抛物线方程,准线方程;
可得抛物线方程,准线方程;
(2)显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,
,![]() ,直线
,直线![]() 方程与抛物线方程联立消元应用韦达定理得
方程与抛物线方程联立消元应用韦达定理得![]() ,不妨设
,不妨设![]() 在第二象限,
在第二象限,![]() 在第一象限,由
在第一象限,由![]() 在第四象限,
在第四象限,![]() 在第三象限,设
在第三象限,设![]() ,
,![]() ,由
,由![]() 坐标求出
坐标求出![]() ,
,
然后计算![]() 得
得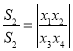 ,代入化简得
,代入化简得![]() ,从而易得最小值及直线方程.
,从而易得最小值及直线方程.
(1)由已知![]() ,
,![]() ,所以抛物线方程为
,所以抛物线方程为![]() ,准线方程为
,准线方程为![]() .
.
(2)显然直线![]() 的斜率存在,设直线
的斜率存在,设直线![]() 方程为
方程为![]() ,
,![]() ,
,
由![]() 得
得![]() ,所以
,所以![]() ,
,![]() ,
,
如图.不妨设![]() 在第二象限,
在第二象限,![]() 在第一象限,由
在第一象限,由![]() 在第四象限,
在第四象限,![]() 在第三象限,设
在第三象限,设![]() ,
,![]() ,
,
直线![]() 方程为
方程为![]() ,由
,由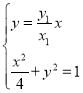 得,
得,![]() ,由
,由![]() ,所以
,所以![]() ,
,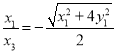 ,同理
,同理![]() ,
,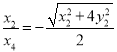
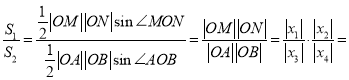
![]()
![]()
![]()
![]()
![]()
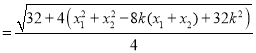
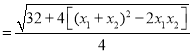
![]() ,
,
所以![]() 时,
时,![]() 取得最小值2.此时直线
取得最小值2.此时直线![]() 方程为
方程为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】为了响应绿色出行,某市推出了新能源分时租赁汽车,并对该市市民使用新能源租赁汽车的态度进行调查,得到有关数据如下表1:
表1
愿意使用新能源租赁汽车 | 不愿意使用新能源租赁汽车 | 总计 | |
男性 | 100 | 300 | |
女性 | 400 | ||
总计 | 400 |
其中一款新能源分时租赁汽车的每次租车费用由行驶里程和用车时间两部分构成:行驶里程按1元/公里计费;用车时间不超过30分钟时,按0.15元/分钟计费;超过30分钟时,超出部分按0.20元/分钟计费.已知张先生从家到上班地点15公里,每天上班租用该款汽车一次,每次的用车时间均在20~60分钟之间,由于堵车红绿灯等因素,每次的用车时间![]() (分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
(分钟)是一个随机变量.张先生记录了100次的上班用车时间,并统计出在不同时间段内的频数如下表2:
表2
时间 | (20,30] | (30,40] | (40,50] | (50,60] |
频数 | 20 | 40 | 30 | 10 |
(1)请补填表1中的空缺数据,并判断是否有99.5%的把握认为该市市民对新能源租赁汽车的使用态度与性别有关;
(2)根据表2中的数据,将各时间段发生的频率视为概率,以各时间段的区间中点值代表该时间段的取值,试估计张先生租用一次该款汽车上班的平均用车时间;
附: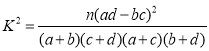
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |