题目内容
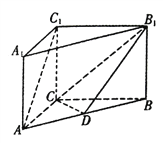
【题目】如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线AC的长为10![]() cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
cm,容器Ⅱ的两底面对角线EG,E1G1的长分别为14cm和62cm. 分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm. 现有一根玻璃棒l,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)
(1)将l放在容器Ⅰ中,l的一端置于点A处,另一端置于侧棱CC1上,求l没入水中部分的长度;
(2)将l放在容器Ⅱ中,l的一端置于点E处,另一端置于侧棱GG1上,求l没入水中部分的长度.
【答案】(1)16cm.(2)20cm.
【解析】
试题(1)转化为直角三角形ACM中,利用相似性质求解AP1;(2)转化到三角形EGN中,先利用直角梯形性质求角![]() ,再利用正弦定理求角
,再利用正弦定理求角![]() ,最后根据直角三角形求高,即为
,最后根据直角三角形求高,即为![]() 没入水中部分的长度.
没入水中部分的长度.
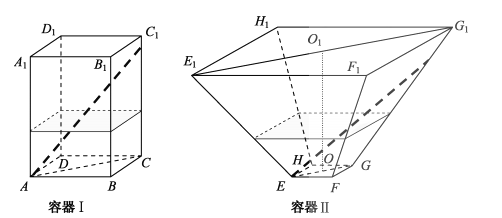
试题解析:解:(1)由正棱柱的定义,![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() ,
,![]() .
.
记玻璃棒的另一端落在![]() 上点
上点![]() 处.
处.
因为![]() ,
,
所以![]() ,从而
,从而 ![]() ,
,
记![]() 与水面的焦点为
与水面的焦点为![]() ,过
,过![]() 作P1Q1⊥AC, Q1为垂足,
作P1Q1⊥AC, Q1为垂足,
则 P1Q1⊥平面 ABCD,故P1Q1=12,
从而 AP1= ![]() .
.
答:玻璃棒l没入水中部分的长度为16cm.
( 如果将“没入水中部分冶理解为“水面以上部分冶,则结果为24cm)
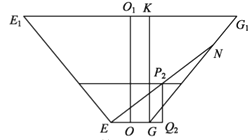
(2)如图,O,O1是正棱台的两底面中心.
由正棱台的定义,OO1⊥平面 EFGH, 所以平面E1EGG1⊥平面EFGH,O1O⊥EG.
同理,平面 E1EGG1⊥平面E1F1G1H1,O1O⊥E1G1.
记玻璃棒的另一端落在GG1上点N处.学科&网
过G作GK⊥E1G,K为垂足, 则GK =OO1=32.
因为EG = 14,E1G1= 62,
所以KG1= ![]() ,从而
,从而![]() .
.
设![]() 则
则![]() .
.
因为![]() ,所以
,所以![]() .
.
在![]() 中,由正弦定理可得
中,由正弦定理可得![]() ,解得
,解得![]() .
.
因为![]() ,所以
,所以![]() .
.
于是![]() .
.
记EN与水面的交点为P2,过 P2作P2Q2⊥EG,Q2为垂足,则 P2Q2⊥平面 EFGH,故P2Q2=12,从而 EP2=![]() .
.
答:玻璃棒l没入水中部分的长度为20cm.
(如果将“没入水中部分冶理解为“水面以上部分冶,则结果为20cm)

【题目】为更好地落实农民工工资保证金制度,南方某市劳动保障部门调查了2018年下半年该市![]() 名农民工(其中技术工、非技术工各
名农民工(其中技术工、非技术工各![]() 名)的月工资,得到这
名)的月工资,得到这![]() 名农民工的月工资均在
名农民工的月工资均在![]() (百元)内,且月工资收入在
(百元)内,且月工资收入在![]() (百元)内的人数为
(百元)内的人数为![]() ,并根据调查结果画出如图所示的频率分布直方图:
,并根据调查结果画出如图所示的频率分布直方图:
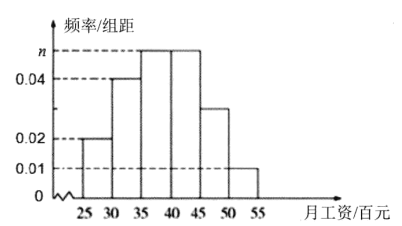
(1)求![]() 的值;
的值;
(2)已知这![]() 名农民工中月工资高于平均数的技术工有
名农民工中月工资高于平均数的技术工有![]() 名,非技术工有
名,非技术工有![]() 名.
名.
①完成如下所示![]() 列联表
列联表
技术工 | 非技术工 | 总计 | |
月工资不高于平均数 |
| ||
月工资高于平均数 |
| ||
总计 |
|
|
|
②则能否在犯错误的概率不超过![]() 的前提下认为是不是技术工与月工资是否高于平均数有关系?
的前提下认为是不是技术工与月工资是否高于平均数有关系?
参考公式及数据: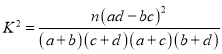 ,其中
,其中![]() .
.
|
|
|
|
|
|
|
|
|
|