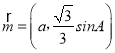题目内容
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
【答案】(Ⅰ) ![]() ;(Ⅱ)存在,
;(Ⅱ)存在,![]()
【解析】
(1)![]() 的值域为
的值域为![]() ,则函数
,则函数![]() 必须是开口向上、与
必须是开口向上、与![]() 轴有唯一交点的二次函数.可以求出
轴有唯一交点的二次函数.可以求出![]() 的值.
的值.
(2)已知某函数零点个数,求参数问题,函数零点问题可以转化为方程根或者通过转化变成两图象交点个数问题.本题中令 ![]() ,则它的图象非常熟悉,而
,则它的图象非常熟悉,而![]() 在
在![]() ∈
∈![]() 的图象则需要考虑是否是二次函数,当确定是二次函数时,考虑函数的开口方向,对称轴与区间的位置关系(为了更好的研究函数在区间的单调性,便于考虑它的性质).
的图象则需要考虑是否是二次函数,当确定是二次函数时,考虑函数的开口方向,对称轴与区间的位置关系(为了更好的研究函数在区间的单调性,便于考虑它的性质).
(Ⅰ)函数![]() 的值域为
的值域为![]() ,则
,则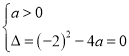 ,解得
,解得![]() .
.
(Ⅱ)由![]() ,
,
即![]()
令![]() ,
,![]() ,
,![]() ∈
∈![]() ,原命题等价于两个函数
,原命题等价于两个函数![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点.
内有唯一交点.
(1)当![]() 时,
时,![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,
上递增,
而g(1)=1>0=h(1),g(2)=-1<1=h(2),
∴函数![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点.
内有唯一交点.
(2)当![]() 时,
时,![]() 图象开口向下,对称轴为
图象开口向下,对称轴为![]() ,
,![]() 在
在![]() 上递减,
上递减,
![]() 在
在![]() 上递增,
上递增,![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点,
内有唯一交点,
当且仅当![]() ,即
,即![]() 即
即![]() .
.
∴![]()
(3)当![]() 时,
时,![]() 图象开口向上,对称轴为
图象开口向上,对称轴为![]() ,
,![]() 在
在![]() 上递减,
上递减,![]() 在
在![]() 上递增,
上递增,![]() 与
与![]() 的图象在
的图象在![]() 内有唯一交点,
内有唯一交点,
![]() ,即
,即![]() 即
即![]() ,
,
∴![]() .
.
综上,存在实数![]() ,使函数
,使函数![]() 于在区间
于在区间![]() 内有且只有一个点.
内有且只有一个点.

练习册系列答案
相关题目