题目内容
12.如图,一个子弹运动的轨迹是一个三次函数图象的一部分,则这个函数的解析式是( )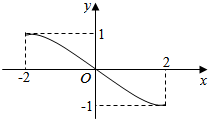
| A. | y=-$\frac{1}{3}$x3+$\frac{5}{6}$x | B. | y=$\frac{1}{3}$x3-$\frac{11}{6}x$ | C. | y=$\frac{2}{3}{x}^{3}$-$\frac{19}{6}x$ | D. | y=$\frac{1}{16}{x}^{3}-\frac{3}{4}x$ |
分析 分别求出四个选项中的导数,验证在x=±2处的导数为0成立与否,即可得出函数的解析式.
解答 解:A中,y=-$\frac{1}{3}$x3+$\frac{5}{6}$x,则y′=-x2+$\frac{5}{6}$,当x=±2时,y′≠0,不满足要求;
B中,y=$\frac{1}{3}$x3-$\frac{11}{6}x$,则y′=-x2-$\frac{11}{6}$,当x=±2时,y′≠0,不满足要求;
C中,y=$\frac{2}{3}{x}^{3}$-$\frac{19}{6}x$,则y′=-2x2-$\frac{19}{6}$,当x=±2时,y′≠0,不满足要求;
D中,y=$\frac{1}{16}{x}^{3}-\frac{3}{4}x$,则y′=$\frac{3}{16}$x2-$\frac{3}{4}$,当x=±2时,y′=0,满足要求;
故选:D
点评 本题考查导数的几何意义,导数几何意义是导数的重要应用

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
2.设随机变量x~N(1,δ2),若P(x>2)=0.3,则P(x>0)等于( )
| A. | 0.3 | B. | 0.4 | C. | 0.6 | D. | 0.7 |
3.复数z=i2+i3(i是虚数单位)在复平面中对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
20. 把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
 把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )
把正整数按一定的规律排成了如图所示的三角形数,设aij(i,j∈N+)是位于这个三角形数中从上往下数第i行,从左往右数第j列的数,如a32=5,若aij=2015,则i+j=( )| A. | 111 | B. | 110 | C. | 108 | D. | 105 |
7.若log23=a,则log49=( )
| A. | $\sqrt{a}$ | B. | a | C. | 2a | D. | a2 |
2.已知向量$\overrightarrow{a}$,$\overrightarrow{b}$均为单位向量,其夹角为θ,给出命题:p:|$\overrightarrow{a}$-$\overrightarrow{b}$|>1;q:θ∈[$\frac{π}{2}$,$\frac{5π}{6}$),则p是q的( )
| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |