题目内容
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )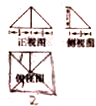
| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |
分析 画出满足条件的几何体,进而求出这个几何体的外接球的半径,代入球的表面积公式,可得答案.
解答 解:如图该几何体为三棱锥,
其直观图如图所示:
由O到棱锥的四个顶点A,B,C,D的距离均为1,
这个几何体的外接球的半径r=1,
∴${S_球}=4π{r^2}=4π$,
故选:C.
点评 本题考查的知识点是由三角形求体积,其中根据已知分析出几何体的形状,进而求出外接球半径,是解答的关键.

练习册系列答案
相关题目
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=1$的渐近线与圆x2+(y-2)2=1相交,则该双曲线的离心率的取值范围是( )
| A. | ($\sqrt{3}$,+∞) | B. | (1,$\sqrt{3}$) | C. | (2.+∞) | D. | (1,2) |
