题目内容
5.设数列{$\frac{{a}_{n}}{n}$}是公差为d的等差数列,若a3=2,a9=12,则d=$\frac{1}{9}$;a12=20.分析 由数列{$\frac{{a}_{n}}{n}$}是公差为d的等差数列,结合已知列式求得公差,再代入等差数列的通项公式求a12.
解答 解:∵数列{$\frac{{a}_{n}}{n}$}是公差为d的等差数列,且a3=2,a9=12,
则$\frac{{a}_{9}}{9}=\frac{{a}_{3}}{3}+6d$,即$\frac{12}{9}=\frac{2}{3}+6d$,解得:d=$\frac{1}{9}$,
∴$\frac{{a}_{12}}{12}=\frac{{a}_{9}}{9}+3×\frac{1}{9}$,即a12=20.
故答案为:$\frac{1}{9}$;20.
点评 本题考查了等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
16.已知复数z满足$\frac{1-2i}{z}$=i,则复数z的共轭复数在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知全集I={1,2,4,6,7,9},其中M={2,4,7,9},P={1,4,7,9},则(∁IM)∩P=( )
| A. | {1,4,6} | B. | {1,6} | C. | {1} | D. | {6} |
10.已知向量$\overrightarrow{a}$=(3,1),$\overrightarrow{b}$=(sinα,cosα),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则tan2α=( )
| A. | $\frac{3}{5}$ | B. | -$\frac{3}{5}$ | C. | $\frac{3}{4}$ | D. | -$\frac{3}{4}$ |
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )
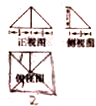

| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |