题目内容
4.已知双曲线x2a2−y2b2=1x2a2−y2b2=1的渐近线与圆x2+(y-2)2=1相交,则该双曲线的离心率的取值范围是( )| A. | (√3√3,+∞) | B. | (1,√3√3) | C. | (2.+∞) | D. | (1,2) |
分析 先根据双曲线方程求得双曲线的渐近线,进而利用圆心到渐近线的距离小于半径求得a和b的关系,进而利用c2=a2+b2求得a和c的关系,则双曲线的离心率可求.
解答 解:∵双曲线渐近线为bx±ay=0,与圆x2+(y-2)2=1相交
∴圆心到渐近线的距离小于半径,即2a√b2+a22a√b2+a2<1
∴3a2<b2,
∴c2=a2+b2>4a2,
∴e=caca>2
故选:C.
点评 本题主要考查了双曲线的简单性质,直线与圆的位置关系,点到直线的距离公式等.考查了学生数形结合的思想的运用.

练习册系列答案
相关题目
12.已知F为双曲线x2a2x2a2-y2b2y2b2=1(a>0,b>0)的右焦点,定点A为双曲线虚轴的一个顶点,过F,A的直线与双曲线的一条渐近线在y轴左侧的交点为B,若→FA−−→FA=(√2√2-1)→AB−−→AB,则此双曲线的离心率是( )
| A. | √2√2 | B. | √3√3 | C. | 2√2√2 | D. | √5√5 |
19.下列函数中既是轴对称又是增函数的是( )
| A. | y=-2x2x | B. | y=2x | C. | y=log2x | D. | y=2x |
16.已知复数z满足1−2iz1−2iz=i,则复数z的共轭复数在复平面内对应的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知全集I={1,2,4,6,7,9},其中M={2,4,7,9},P={1,4,7,9},则(∁IM)∩P=( )
| A. | {1,4,6} | B. | {1,6} | C. | {1} | D. | {6} |
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )
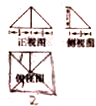

| A. | 4π34π3 | B. | 8π38π3 | C. | 4π | D. | 2π |
