题目内容
16.已知f(x)=log2$\frac{x+2}{x-2}$,g(x)=log2(x-2)+log2(p-x)(p>2),(1)求f(x),g(x)同时有意义的实数x的取值范围;
(2)求F(x)=f(x)+g(x)的值域.
分析 (1)由函数的解析式可得$\left\{\begin{array}{l}{\frac{x+2}{x-2}>0}\\{x-2>0}\\{p-x>0}\end{array}\right.$,由此求得使f(x),g(x)同时有意义的实数x的取值范围.
(2)令t(x)=(x+2)(p-x),2<x<p,则F(x)=log2t(x),求得t的值域,可得F(x)的值域.
解答 解:(1)根据f(x)=log2$\frac{x+2}{x-2}$,g(x)=log2(x-2)+log2(p-x)(p>2),
可得$\left\{\begin{array}{l}{\frac{x+2}{x-2}>0}\\{x-2>0}\\{p-x>0}\end{array}\right.$,求得2<x<p,故f(x),g(x)同时有意义的实数x的取值范围是(2,p).
(2)令F(x)=f(x)+g(x)=log2(x+2)(p-x),
令t(x)=(x+2)(p-x),2<x<p,则F(x)=log2t(x),且0<t(x)≤t($\frac{p-2}{2}$)=${(\frac{p+2}{2})}^{2}$.
∴F(x)≤log2 ${(\frac{p+2}{2})}^{2}$=2log2$\frac{p+2}{2}$=2log2(p+2)-2,即F(x)的值域为(-∞,2log2(p+2)-2).
点评 本题主要考查对数函数的图象和性质,二次函数的性质,体现了转化的数学思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )
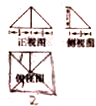

| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |
 如图,O是边长为2的等边△ABC的中心,动点E在边AC上运动,F在边AB及BC上运动,则$\overrightarrow{OB}$•$\overrightarrow{EF}$的取值范围是[0,2].
如图,O是边长为2的等边△ABC的中心,动点E在边AC上运动,F在边AB及BC上运动,则$\overrightarrow{OB}$•$\overrightarrow{EF}$的取值范围是[0,2]. 如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA=SD,∠BAD=60°,AB=2,SE=$\sqrt{3}$,SC=$\sqrt{10}$,E是AD中点,SF=2FC.
如图,在四棱锥S-ABCD中,底面ABCD是菱形,SA=SD,∠BAD=60°,AB=2,SE=$\sqrt{3}$,SC=$\sqrt{10}$,E是AD中点,SF=2FC.