题目内容
3.若正数项数列{an}的前n项和为Sn,a1=1,a2=3,且数列{$\sqrt{{S}_{n}}$}为等差数列.(1)求数列{an}的通项公式;
(2)若a2,a5恰为等比数列{bn}的前两项,且数列{2bn}的前m项和Tm为32015-3,求m的值.
分析 (1)由已知求出等差数列{$\sqrt{{S}_{n}}$}的首项和公差,求出其通项公式,然后利用an=Sn-Sn-1(n≥2)求得数列{an}的通项公式;
(2)由(1)中的通项公式求得a5,得到等比数列的公比,然后求出数列{2bn}的前m项和得答案.
解答 解:(1)∵a1=1,a2=3,∴$\sqrt{{S}_{1}}=\sqrt{{a}_{1}}=1$,$\sqrt{{S}_{2}}=\sqrt{{a}_{1}+{a}_{2}}=\sqrt{1+3}=2$,
∴数列{$\sqrt{{S}_{n}}$}的公差d=2-1=1,
∴$\sqrt{{S}_{n}}=\sqrt{{S}_{1}}+1×(n-1)=1+n-1=n$,
即${S}_{n}={n}^{2}$.
当n≥2时,${a}_{n}={S}_{n}-{S}_{n-1}={n}^{2}-(n-1)^{2}=2n-1$,
n=1适合上式,
∴an=2n-1;
(2)a2=3,a5=2×5-1=9,
∴等比数列{bn}的公比q=3,
则${b}_{n}={b}_{1}{q}^{n-1}=3×{3}^{n-1}={3}^{n}$,
∴数列{2bn}的前m项和Tm=$2×\frac{3(1-{3}^{m})}{1-3}={3}^{m+1}-3$,
由3m+1-3=32015-3,得m=2014.
点评 本题考查了等差数列的通项公式,考查了等比关系的确定,考查了等比数列的前n项和,是中档题.

练习册系列答案
 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案
相关题目
13.已知全集I={1,2,4,6,7,9},其中M={2,4,7,9},P={1,4,7,9},则(∁IM)∩P=( )
| A. | {1,4,6} | B. | {1,6} | C. | {1} | D. | {6} |
14.一个几何体的三视图如图所示,则这个几何体的外接球的表面积为 ( )
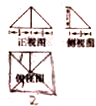

| A. | $\frac{4π}{3}$ | B. | $\frac{8π}{3}$ | C. | 4π | D. | 2π |
8.化简$\frac{\sqrt{3}}{4}$tan10°+sin10°=( )
| A. | 1 | B. | $\sqrt{3}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{4}$ |