题目内容
【题目】已知二项式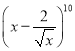
的展开式.
(1)求展开式中含
项的系数；
(2)如果第
项和第
项的二项式系数相等，求
的值．
【答案】（1）
；（2）1
【解析】试题分析：（1）写出二项展开式的通项公式，当
的指数是
时，可得到关于
方程，解方程可得
的值，从而可得展开式中含
项的系数；（2）根据上一问写出的通项公式，利用第
项和第
项的二项式系数相等，可得到一个关于
的方程，解方程即可得结果.
试题解析：(1)设第k＋1项为Tk＋1＝
令10－
k＝4，解得k＝4，
故展开式中含x4项的系数为
3 360.
(2)∵第3r项的二项式系数为
，第r＋2项的二项式系数为
，
∵ ＝，故3r－1＝r＋1或3r－1＋r＋1＝10，
解得r＝1或r＝2.5(不合题意，舍去)，∴r＝1.
练习册系列答案
相关题目
