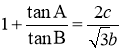题目内容
【题目】在平面直角坐标系xOy中.直线1的参数方程为
（t为参数）.在以坐标原点为极点，x轴的非负半轴为极轴的极坐标系中.曲线C的极坐标方程为ρ＝2cosθ.
（1）若曲线C关于直线l对称，求a的值；
（2）若A、B为曲线C上两点.且∠AOB
，求|OA|+|OB|的最大值.
【答案】（1）a＝0（2）2
【解析】
（1）直接利用转换关系式，把参数方程极坐标方程和直角坐标方程之间进行转换．
（2）利用三角函数关系式的恒等变换和正弦型函数的性质的应用及极径的应用求出结果．
（1）直线1的参数方程为
（t为参数）.转换为直角坐标方程为x
.
曲线C的极坐标方程为ρ＝2cosθ，整理得ρ2＝2ρcosθ，转换为直角坐标方程为x2+y2＝2x，转换为（x﹣1）2+y2＝1.
由于曲线关于直线l对称，所以圆心（1，0）在直线l上，
故a＝0.
（2）由点A、B在圆ρ＝2cosθ上，且∠AOB
，
所以设∠AOx＝α，
，
，
则：|OA|+|OB|＝2cos
，当且仅当
时，等号成立.
故OA|+|OB|的最大值为2
.
练习册系列答案
相关题目
