题目内容
【题目】已知数列![]() ,
,![]() 均为各项都不相等的数列,
均为各项都不相等的数列,![]() 为
为![]() 的前n项和,
的前n项和,![]() .
.
![]() 若
若![]() ,求
,求![]() 的值;
的值;
![]() 若
若![]() 是公比为
是公比为![]() 的等比数列,求证:数列
的等比数列,求证:数列![]() 为等比数列;
为等比数列;
![]() 若
若![]() 的各项都不为零,
的各项都不为零,![]() 是公差为d的等差数列,求证:
是公差为d的等差数列,求证:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列的充要条件是
成等差数列的充要条件是![]() .
.
【答案】(1)8;(2)证明见解析(3)证明见解析
【解析】
![]() 直接代入计算即可;
直接代入计算即可;
![]() 通过设
通过设![]() ,利用等比数列的求和公式及
,利用等比数列的求和公式及![]() ,计算可知
,计算可知![]() ,进而化简即得结论;
,进而化简即得结论;
![]() 通过数列
通过数列![]() 是公差为
是公差为![]() 的等差数列,对
的等差数列,对![]() 变形可知
变形可知![]() ,然后分别证明充分性、必要性即可.
,然后分别证明充分性、必要性即可.
解:![]() ,
,![]() ,
,![]() ,
,
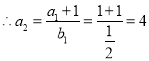 ,
,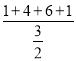
![]() ,
,
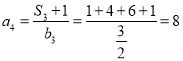 ,
,
证明:![]() 设
设![]() ,则
,则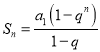 ,
,
![]() ,
,
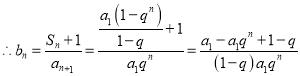 ,
,
![]()
![]()
![]() ,
,![]() 为常数
为常数![]()
![]() 数列
数列![]() 为等比数列,
为等比数列,
![]() 数列
数列![]() 是公差为d的等差数列,
是公差为d的等差数列,
![]() 当
当![]() 时,
时,![]() ,
,
即![]() ,
,
![]() 数列
数列![]() 的各项都不为零,
的各项都不为零,
![]() ,
,![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,
,
两式相减得:当![]() 时,
时,![]() .
.
先证充分性:
由![]() 可知
可知![]() ,
,
![]() 当
当![]() 时,
时,![]() ,
,
又![]() ,
,
![]() ,
,
即![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列;
成等差数列;
再证必要性:
![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
![]() 当
当![]() 时,
时,![]() ,
,
![]() ,
,
![]() .
.
综上所述,![]() ,
,![]() ,
,![]() ,
,![]() 成等差数列的充要条件是
成等差数列的充要条件是![]()

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目