题目内容
【题目】在平面直角坐标系xOy中,以坐标原点O为极点,以x轴正半轴为极轴,建立极坐标系,曲线C的极坐标方程为![]() 射线
射线![]() 交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
交曲线C于点A,倾斜角为α的直线l过线段OA的中点B且与曲线C交于P、Q两点.
(1)求曲线C的直角坐标方程及直线l的参数方程;
(2)当直线l倾斜角α为何值时, |BP|·|BQ|取最小值, 并求出|BP|·|BQ|最小值.
【答案】(1)曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数))(2)当
为参数))(2)当![]() 时,
时,![]() 取得最小值为
取得最小值为![]()
【解析】
(1)由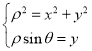 求得曲线
求得曲线![]() 的直角坐标方程;先求出曲线
的直角坐标方程;先求出曲线![]() 与直线
与直线![]() 的交点
的交点![]() 的坐标,即可得到
的坐标,即可得到![]() 的中点
的中点![]() ,进而求解即可;
,进而求解即可;
(2)由(1),将直线![]() 的参数方程代入到曲线
的参数方程代入到曲线![]() 的直角坐标方程中,由参数的几何意义可得
的直角坐标方程中,由参数的几何意义可得![]() ,进而求解即可.
,进而求解即可.
(1)由题,因为![]() ,即
,即![]() ,
,
因为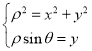 ,
,
所以![]() ,即
,即![]() ,
,
则曲线![]() 的直角坐标方程为
的直角坐标方程为![]() ,
,
因为射线![]() 交曲线
交曲线![]() 于点
于点![]() ,所以点
,所以点![]() 的极坐标为
的极坐标为![]() ,
,
则点![]() 的直角坐标为
的直角坐标为![]() ,所以
,所以![]() 的中点
的中点![]() 为
为![]() ,
,
所以倾斜角为![]() 且过点
且过点![]() 的直线
的直线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).
为参数).
(2)将直线![]() 的参数方程
的参数方程![]() (
(![]() 为参数)代入曲线
为参数)代入曲线![]() 的方程
的方程![]() 中,
中,
整理可得![]() ,
,
设![]() 、
、![]() 对应的参数值分别是
对应的参数值分别是![]() 、
、![]() ,则有
,则有![]() ,
,
则![]() ,
,
因为![]() ,当
,当![]() ,即
,即![]() 时,
时,![]() 取得最小值为
取得最小值为![]()

 名校课堂系列答案
名校课堂系列答案【题目】某校高三共有1000位学生,为了分析某次的数学考试成绩,采取随机抽样的方法抽取了50位高三学生的成绩进行统计分析,得到如图所示频数分布表:
分组 |
|
|
|
|
|
频数 | 3 | 11 | 18 | 12 | 6 |
(1)根据频数分布表计算成绩在![]() 的频率并计算这组数据的平均值
的频率并计算这组数据的平均值![]() (同组的数据用该组区间的中点值代替);
(同组的数据用该组区间的中点值代替);
(2)用分层抽样的方法从成绩在![]() 和
和![]() 的学生中共抽取5人,从这5人中任取2人,求成绩在
的学生中共抽取5人,从这5人中任取2人,求成绩在![]() 和
和![]() 中各有1人的概率.
中各有1人的概率.
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验,并获得了煤气开关旋钮旋转的弧度数![]() 与烧开一壶水所用时间
与烧开一壶水所用时间![]() 的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
的一组数据,且作了一定的数据处理(如下表),得到了散点图(如下图).
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中![]() ,
,![]() .
.
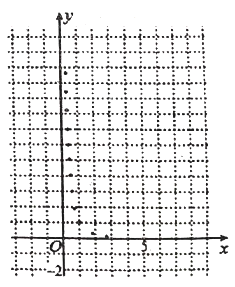
(1)根据散点图判断,![]() 与
与![]() 哪一个更适宜作烧水时间
哪一个更适宜作烧水时间![]() 关于开关旋钮旋转的弧度数
关于开关旋钮旋转的弧度数![]() 的回归方程类型?(不必说明理由)
的回归方程类型?(不必说明理由)
(2)根据判断结果和表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)若单位时间内煤气输出量![]() 与旋转的弧度数
与旋转的弧度数![]() 成正比,那么,利用第(2)问求得的回归方程知
成正比,那么,利用第(2)问求得的回归方程知![]() 为多少时,烧开一壶水最省煤气?
为多少时,烧开一壶水最省煤气?
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计值分别为
的斜率和截距的最小二乘法估计值分别为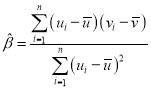 ,
,![]()
【题目】某人沿固定路线开车上班,沿途共有![]() 个红绿灯,他对过去
个红绿灯,他对过去![]() 个工作日上班途中的路况进行了统计,得到了如表的数据:
个工作日上班途中的路况进行了统计,得到了如表的数据:
上班路上遇见的红灯数 |
|
|
|
|
|
|
天数 |
|
|
|
|
|
|
若一路绿灯,则他从家到达公司只需用时![]() 分钟,每遇一个红灯,则会多耗时
分钟,每遇一个红灯,则会多耗时![]() 分钟,以频率作为概率的估计值
分钟,以频率作为概率的估计值
(1)试估计他平均每天上班需要用时多少分钟?
(2)若想以不少于![]() 的概率在早上
的概率在早上![]() 点前(含
点前(含![]() 点)到达公司,他最晚何时要离家去公司?
点)到达公司,他最晚何时要离家去公司?
(3)公司规定,员工应早上![]() 点(含
点(含![]() 点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款
点)前打卡考勤,否则视为迟到,每迟到一次,会被罚款![]() 元.因某些客观原因,在接下来的
元.因某些客观原因,在接下来的![]() 个工作日里,他每天早上只能
个工作日里,他每天早上只能![]() 从家出发去公司,求他因迟到而被罚款的期望.
从家出发去公司,求他因迟到而被罚款的期望.
