题目内容
【题目】设等差数列{an}的前n项和为Sn，且a3+2S6＝77，a10﹣a5＝10.
（1）求数列{an}的通项公式；
（2）数列{bn}满足：b1＝1，bn﹣bn﹣1＝an﹣n+1（n≥2），求数列{
}的前n项和Tn.
【答案】（1）an＝2n﹣1（2）
【解析】
（1）联立解方程组，得
，求出通项公式即可；
（2）求出
，利用裂项相消法求出数列
的前
项和
．
（1）等差数列{an}的前n项和为Sn，且a3+2S6＝77，a10﹣a5＝10，
，得，
故an＝2n﹣1；
（2）b1＝1，bn﹣bn﹣1＝an﹣n+1＝n（n≥2），
∴bn＝（bn﹣bn﹣1）+（bn﹣1﹣bn﹣2）+…+（b2﹣b1）+b1＝n+n﹣1+…+2+1
，
当n＝1时，显然成立，
，
数列{
}的前n项和Tn＝8（
）＝8（1
）
.
练习册系列答案
阅读快车系列答案
相关题目
【题目】某学生为了测试煤气灶烧水如何节省煤气的问题设计了一个实验，并获得了煤气开关旋钮旋转的弧度数
与烧开一壶水所用时间
的一组数据，且作了一定的数据处理（如下表），得到了散点图（如下图）.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
表中
，
.
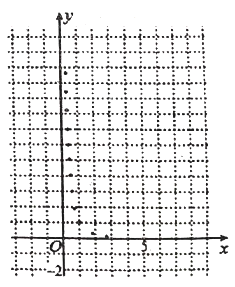
（1）根据散点图判断，
与
哪一个更适宜作烧水时间关于开关旋钮旋转的弧度数的回归方程类型？（不必说明理由）
（2）根据判断结果和表中数据，建立关于的回归方程；
（3）若单位时间内煤气输出量
与旋转的弧度数成正比，那么，利用第（2）问求得的回归方程知为多少时，烧开一壶水最省煤气？
附：对于一组数据
，其回归直线
的斜率和截距的最小二乘法估计值分别为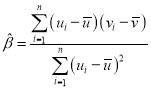
，