题目内容
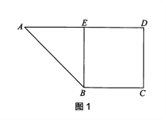
【题目】如图1,梯形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点.将
中点.将![]() 沿
沿![]() 翻折到
翻折到![]() 的位置,使
的位置,使![]() ,如图2.
,如图2.
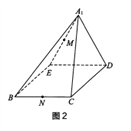
(Ⅰ)求证:平面![]() 与平面
与平面![]() ;
;
(Ⅱ)求直线![]() 与平面
与平面![]() 所成角的正弦值;
所成角的正弦值;
(Ⅲ)设![]() 分别为
分别为![]() 和
和![]() 的中点,试比较三棱锥
的中点,试比较三棱锥![]() 和三棱锥
和三棱锥![]() (图中未画出)的体积大小,并说明理由.
(图中未画出)的体积大小,并说明理由.
【答案】(Ⅰ)见解析(Ⅱ)![]() (Ⅲ)见解析
(Ⅲ)见解析
【解析】试题分析:(1)由题意易知: ![]() ,
, ![]() ,所以
,所以![]() 平面
平面![]() ,从而得证;(2)建立空间坐标系,平面
,从而得证;(2)建立空间坐标系,平面![]() 的法向量为
的法向量为![]() ,代入公式即可求得;(3)利用向量法证明
,代入公式即可求得;(3)利用向量法证明![]() 平面
平面![]() ,所以三棱锥
,所以三棱锥![]() 和三棱锥
和三棱锥![]() 的体积大小相同.
的体积大小相同.
试题解析:
(Ⅰ)证明:因为![]() ,
, ![]() ,
, ![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]()
(Ⅱ)解:在平面![]() 内作
内作![]() ,
,
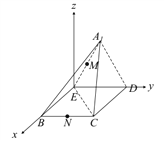
由![]() 平面
平面![]() ,建系如图.
,建系如图.
则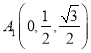 ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.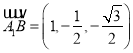 ,
,
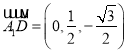 ,
, ![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则
![]() ,即
,即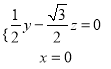 ,
,
令![]() 得,
得, ![]() ,
,
所以![]() 是平面
是平面![]() 的一个法向量.
的一个法向量.
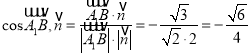 ,
,
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(Ⅲ)解:三棱锥![]() 和三棱锥
和三棱锥![]() 的体积相等.
的体积相等.
理由如:由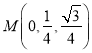 ,
, ![]() ,
,
知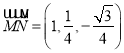 ,则
,则![]()
因为![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]()
故点![]() 到平面
到平面![]() 的距离相等,有三棱锥
的距离相等,有三棱锥![]() 和
和![]() 同底等高,
同底等高,
所以体积相等.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() (万元)和销售额
(万元)和销售额![]() (万元)的数据统计如下表:
(万元)的数据统计如下表:
城市 |
|
|
|
|
|
|
|
广告费支出 |
|
|
|
|
|
|
|
销售额 |
|
|
|
|
|
|
|
(Ⅰ)若用线性回归模型拟合![]() 与
与![]() 关系,求
关系,求![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(Ⅱ)若用对数函数回归模型拟合![]() 与
与![]() 的关系,可得回归方程
的关系,可得回归方程![]() ,经计算对数函数回归模型的相关系数约为
,经计算对数函数回归模型的相关系数约为![]() ,请说明选择哪个回归模型更合适,并用此模型预测
,请说明选择哪个回归模型更合适,并用此模型预测![]() 城市的广告费用支出
城市的广告费用支出![]() 万元时的销售额.
万元时的销售额.
参考数据: ![]() ,
, ![]() ,
, ![]() ,
, 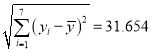 ,
, ![]() ,
, ![]() .
.
参考公式: 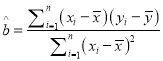 ,
, ![]() .
.
相关系数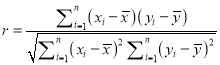 .
.