题目内容
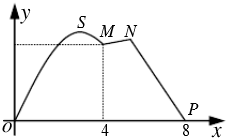
3.如图所示,某市拟在长为8km道路OP的一侧修建一条运动赛道,赛道的前一部分为曲线段OSM,该曲线段为函数y=Asinωx(A>0,ω>0)(x∈[0,4])的图象,且图象的最高点为S(3,2$\sqrt{3}$),赛道的后一部分为折线段MNP,且∠MNP=120°(1)求M、P两点间的直线距离;
(2)求折线段赛道MNP长度的最大值.
分析 (1)由题意结合图象求得A和T,进一步求出ω,则函数解析式可求,代入M的横坐标求得的坐标,由两点间的距离公式求得MP的值;
(2)在△MNP中,设出∠PMN=θ,由正弦定理把PN、MN用含θ的代数式表示,化简后利用三角函数求得最值.
解答 解: (1)依题意,有A=$2\sqrt{3}$,
(1)依题意,有A=$2\sqrt{3}$,
又$\frac{T}{4}=3$,T=12,∴ω=$\frac{2π}{T}=\frac{2π}{12}=\frac{π}{6}$,
∴y=$2\sqrt{3}sin\frac{π}{6}x$,
当x=4时,$y=2\sqrt{3}sin\frac{π}{6}×4=2\sqrt{3}×\frac{\sqrt{3}}{2}=3$.
∴M(4,3),又P(8,0),
∴MP=$\sqrt{{4}^{2}+{3}^{2}}=5$;
(2)在△MNP中,
∠MNP=120°,MP=5,设∠PMN=θ,则0°<θ<60°,
由正弦定理得:$\frac{MP}{sin120°}=\frac{NP}{sinθ}=\frac{MN}{sin(60°-θ)}$,
∴$PN=\frac{10\sqrt{3}}{3}sinθ$,$MN=\frac{10\sqrt{3}}{3}sin(60°-θ)$,
故NP+MN=$\frac{10\sqrt{3}}{3}sinθ+\frac{10\sqrt{3}}{3}sin(60°-θ)$=$\frac{10\sqrt{3}}{3}sin(60°+θ)$.
∵0°<θ<60°,
∴当θ=30°时,折线段赛道MNP最长.
点评 本题考查y=Asin(ωx+φ)的图象的求法,训练了利用正余弦定理求解三角形,是中档题.

练习册系列答案
相关题目
11.在△ABC中,∠A=45°,∠C=105°,BC=$\sqrt{2}$则AC为( )
| A. | $\sqrt{3}-1$ | B. | 1 | C. | 2 | D. | $\sqrt{3}+1$ |